. Let A be the centre of the circle $x^{2} + y^{2} - 2 x - 4 y - 20 = 0$ Suppose that the tangents at the points B(1,7) and D(4,-2) on the circle meet at the point C. Find the area of the quadrilateral ABCD

Video Solution

Text Solution

Verified by Experts

Equation of tangents at (1, 7) and (4, -2) are

$x + 7 y - (x + 1) - 2 (y + 7) - 20 = 0$
$\Rightarrow 5 y = 35 \Rightarrow y = 7$
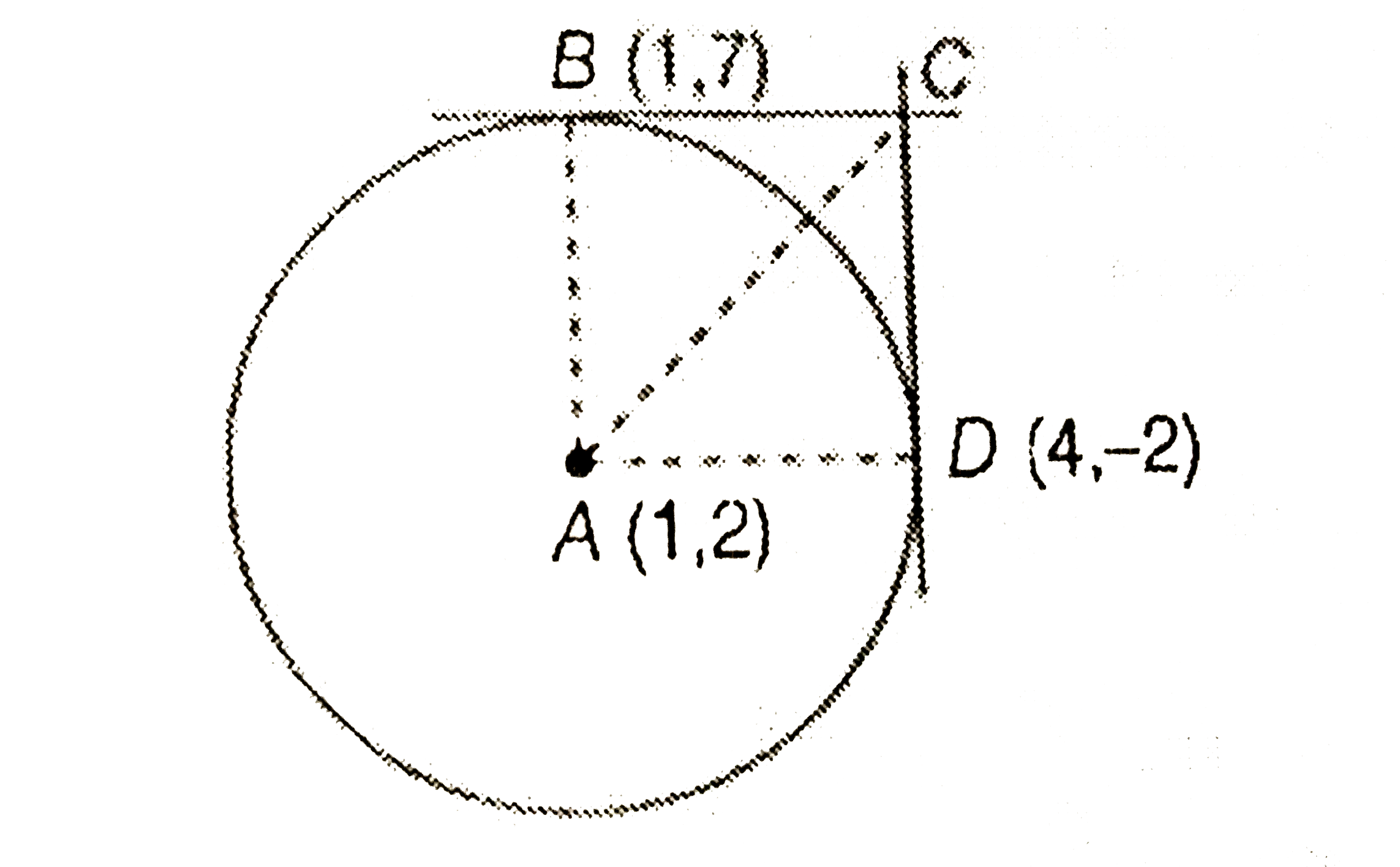
and $4 x - 2 y - (x + 4) - 2 (y - 2) - 20 = 0$
$\Rightarrow 3 x - 4 y = 20$
$∴$ Point C is (16, 7).
$∴$ Vertices of a quadrilateral are
$A (1, 2) B (1, 7), C (16, 7), D (4, - 2)$
$∴$ Area of quadrilateral ABCD
$= Area of Δ A B C + Area of Δ A C D$
$= \frac{1}{2} \times 15 \times 5 + \frac{1}{2} \times 15 \times 5 = 75$ sq units.

Updated on:21/07/2023