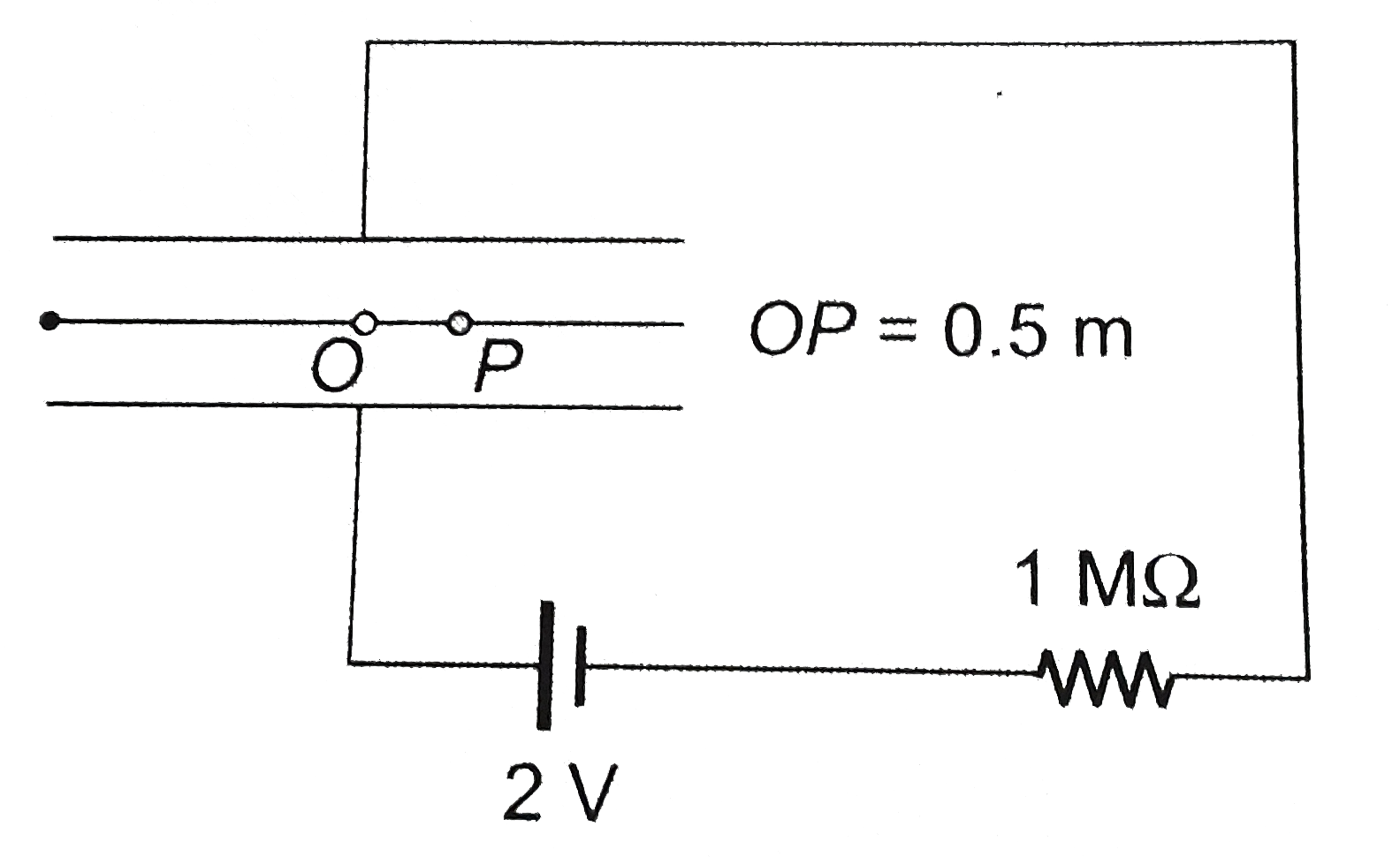
A parallel plate capacitor with circular plates of radius 1m has a capacitor of 1nF. At t=0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery. Calculate the magnetic field at a point P, halfway between the cnetre and the periphery of the plates, after t=10−3sec.
 Solution in Tamil
Solution in Tamil
The time constant of the CR circuit is τ=CR=10−3s. Then, we have
q(t)=CV[1−exp(−t/τ)]
=2×10−9[1−exp (−t/10−3)]
The electric field in between the plates at time t is
E=q(t)ε0A=qπε0,A=π(1)2m2= area of the plates.
Consider now a circular loop of radius (1/2) m parallel to the plates passing through P. The magnetic field B at all points on the loop is along the loop and of the same value. The flux ΦE through this loop is
ΦE=E× area of the loop
=E×π×(12)2=πE4=q4ε0
The displacement current
id=ε0dΦEdt=14dqdt=0.5×10−6 exp (−1)
at t=10−3s. Now, applying Ampere-Maxwell law to the loop, we get
B×2π×(12)=μ0(ic+id)=μ0(0+id)=0.5×10−6μ0 exp(−1)
or, B=0.74×10−13T
Similar Questions
A parallel plate capacitor with circular plates of radius 1m has a capacitance of 1nF. At t = 0, it is connected for chargeing in series with a resistor R=1 M Omega across a 2V battery (Figure). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10^(-3)s . (The charge on the capacitor at time t is q(t)=CV[1-exp((-t)/(tau))] , where the time constant tau is equal to CR).
View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)

View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)
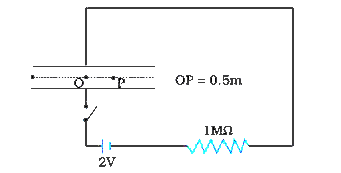
View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)

View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitor of 1nF. At t=0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery. Calculate the magnetic field at a point P, halfway between the cnetre and the periphery of the plates, after t=10−3sec.

View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MO¬a across a 2V battery. Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 - exp (−t/τ)], where the time constant τ is equal to CR.)

View SolutionA parallel plate capacitor with circular plates of radius 0.8 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R = 1 M Omega across a 4V battery. Calculate the magnetic field at a point P, halfway between the centre and the perpendicular of the plates after t=10^(-3)s . (The charge on the capacitor at time t is q (t) = CV [1 - exp (-t//tau) ], where the time constant tau is equal to CR.)
View SolutionA parallel plate capacitor with circular plates o f radius lm has a capacitance o f 1 nF. At 1=0, it is connected fo r charging in series with a resistor R = IM omega across a 2V battery. Calculate the magnetic field at a point P, halfway between the centre and the periphery o f the plates, after t = 10^(-3) s. (The charge on the capacitor at time t is q(t) = CV[1- exp ( t//tau )], where the time constant tau is equal to CR)
View Solution
