The motion of a particle executing simple harmonic motion is described by the displacement function,
x(t)=Acos(ωt+ϕ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM : x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions.Solution in Bengali
A=√2cm,ϕ=7π/4,B=√2cm,a=π/4
Topper's Solved these Questions
- BOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises6videos
OSCILLATIONS
- BOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises6videos
OSCILLATIONS
- BOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES5videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT BANGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)3videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
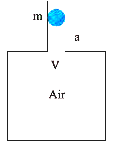
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
 07:35View Solution
07:35View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
 06:53View Solution
06:53View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49ms−1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5ms−1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands ?
03:07View SolutionThe instantaneous speed of the point of contact during rolling is zero.
05:39View SolutionThe motion of a particle in S.H.M. is described by the displacement function, x=Acos(omegat+phi) , If the initial (t=0) position of the particle is 1cm and its initial velocity is omega cm s^(-1) , what are its amplitude and initial phase angle ? The angular frequency of the particle is pis^(-1) . If instead of the cosine function, we choos the sine function to describe the SHM : x=B sin(omegat+alpha) , what are the amlitude and intial phase of the particle with the above intial conditions ?
09:03View Solutionसरल आवर्त गति करते किसी कण की गति का वर्णन निचे दिए गए विस्थापन फलन द्वारा किया जाता हैं, x(t)=Acos(ωt+ϕ) यदि कण की आरंभिक (t = 0) स्थिति 1 cm तथा उसकी आरंभिक वेग πcm s−1 हैं, तो कोण का आयाम तथा आरंभिक कला कोण क्या हैं ? कण की कोणीय आवृत्ति π s−1 हैं | यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या (cos) फलन के स्थान पर हम ज्या फलन चुनें x=Bsin(ωt+α) तो उपरोक्त आरंभिक प्रतिबंधों में कोण का आयाम तथा आरंभिक कला कोण क्या होगा ?
08:29View SolutionA particle executing SHM is described by the displacement function x(t)=Acos(ωt+ϕ), if the initial (t=0) position of the particle is 1 cm, its initial velocity is πi cm s−1 and its angular frequency is πs−1, then the amplitude of its motion is
10:05View SolutionA particle is SHM is described by the displacement function. x = A cos(omega t + phi), "where," omega = 2pi//T If the initial (t = 0) position of the particle is 1 cm and its initial velocity is pi cms^(-1) , what is the initial phase angle ? The angular frequency of the particle is pi s^(-1) .
04:52View Solutionसरल आवर्त गति करते किसी कण की गति का वर्णन नीचे दिए गए विस्थापन फलन द्वारा किया गया है,
x(t)=Acos(ωt+ϕ)
यदि कण की आरंभिक ( t = 0 ) स्थिति 1 सेमी तथा उसका आरंभिक वेग π सेमी/सेकण्ड है, तो कण का आयाम तथा आरंभिक कला कोण क्या है ? कण की कोणीय आवृत्ति π प्रति/सेकण्ड है | यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या ( cos ) फलन के स्थान पर हम ज्या ( sin ) फलन चुनें ,x=bsin(ω1+alphla), तो उपरोक्त आरंभिक प्रतिबंधों में कण का आयाम तथा आरंभिक कला कोण क्या होगा ?04:52View Solutionसरल आवर्त गति करते हुए किसी कण की गति का वर्णन नीचे दिए गए विस्थापन फलन द्वारा किया जाता है -
x(t)=Acos(ωt+ϕ)
यदि कण की आरंभिक(t = 0) स्थिति 1 cm तथा उसका आरंभिक वेगπcm s−1 है , कण का आया तथा आरंभिक कला कौन क्या है ? कण की कोणीय आवृत्ति πs−1 है यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या (cos ) फलन के स्थान पर हम ज्या(sin) फलन चुने x=Bsin(ωt+α) तो उपर्युक्त आरंभिक प्रतिबंधों में कण का आयाम तथा आरंभिक कला क्या होगा ?View Solutionसरल आवर्त गति करते किसी कण की गति का वर्णन नीचे दिये गये विस्थापन फलन द्वारा किया जाता है,
x(t)=Acos(ωt+ϕ) यदि कण की आरंभिक (t=0) स्थिति 1 सेमी. तथा उसका आरम्भिक वेग π cm/s है, तो कण का आयाम तथा आरंभिक कला कोण क्या है? कण की कोणीय आवृत्ति π/s है। यदि सरल आवर्त गति का वर्णन करने के लिये कोज्या (cos) फलन के स्थान पर हम ज्या (sin) फलन चुनें, x=Bsin(ωt+α) तो उपरोक्त आरंभिक प्रतिबंधों में कण का आयाम तथा आरंभिक कला कोण क्या होगा?05:40View SolutionThe motion of a particle executing simple harmonic motion is described by the displacement function,
x(t)=Acos(ωt+ϕ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM : x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions.View SolutionThe motion of a particle executing simple harmonic motion is described by the displacement function,
x(t)=Acos(ωt+ϕ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM : x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions.03:28View SolutionThe motion of a particle executing simple harmonic motion is described by the displacement function,
x(t)=Acos(ωt+ϕ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM : x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions.View SolutionThe motion of a particle executing simple harmonic motion is described by the displacement function, x(t)=Acos(omegat+phi) . If the initial (t = 0) position of the particle is 1 cm and its initial velocity is omega cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is pi s^(-1) . If instead of the cosine function, we choose the sine function to describe the SHM : x = B sin (omegat + alpha) , what are the amplitude and initial phase of the particle with the above initial conditions.
View Solution

