Two uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown . The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
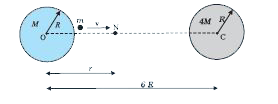 Solution in Bengali
Solution in Bengali
The projectile is acted upon by two mutually opposing gravitational forces of the two spheres. The neutral point N (see Fig. 8.10) is defined as the position where the two forces cancel each other exactly. If ON = r, we have
GMmr2=4GMm(6R−r)2
(6R−r)2=4r2
6 R - r = ± 2r
r = 2R or - 6R.
The neutral point r = – 6R does not concern us in this example. Thus ON = r = 2R. It is sufficient to project the particle with a speed which would enable it to reach N. Thereafter, the greater gravitational pull of 4M would suffice. The mechanical energy at the surface of M is
Ei=12mv2−GMmR−4GMm5R .
At the neutral point N, the speed approaches zero. The mechanical energy at N is purely potential.
EN=−GMm2R−4GMm4R.
From the principle of conservation of mechanical energy
12v2−GMR−4GM5R=−GM2R−GMR
or
v2=2GMR(45−12)
v=(3GM5R)1/2
A point to note is that the speed of the projectile is zero at N, but is nonzero when it strikes the heavier sphere 4 M. The calculation of this speed is left as an exercise to the students.
Topper's Solved these Questions
Similar Questions
You can shled a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means ?
13:19View SolutionAs you have learnt in the text, a geostationary satellite orbits the earth at a height of nearly 36,000 km from the surface of the earth. What is the potential due to earth’s gravity at the site of this satellite ? (Take the potential energy at infinity to be zero). Mass of the earth =6.0×1024kg. radius=6400km .
02:41View SolutionA metre long narrow bore held horizontally (and closed at one end) contains a 76 cm long mercury thread, which traps a 15 cm column of air. What happens if the tube is held vertically with the open end at the bottom ?
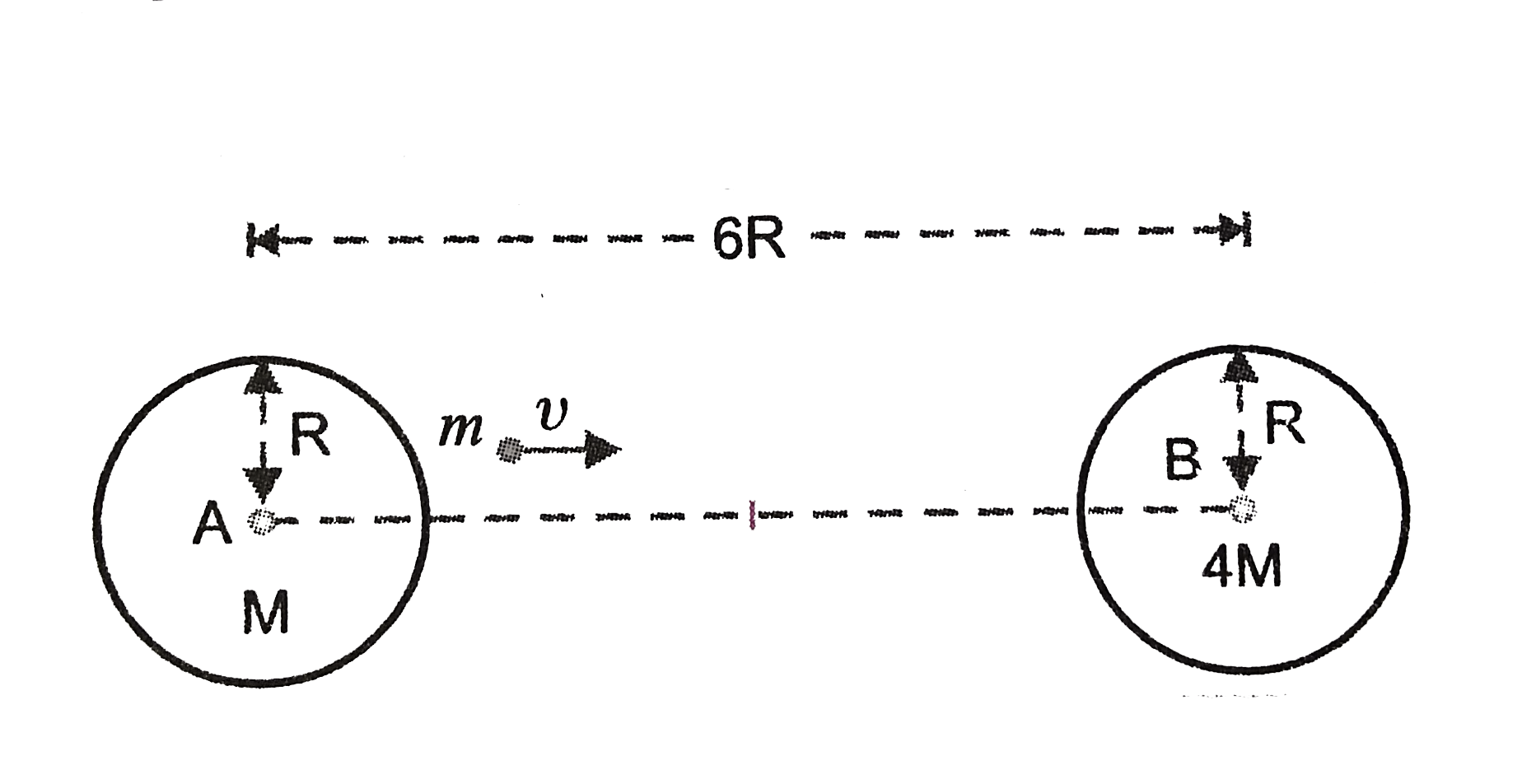
13:19View SolutionTwo uniform soild spheres of equal radii R but mass M and 4M have a centre to centre separation 6R, as shows in Fig. (a) The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of ten second. Obtain an expression for the minimum speed υ of the projectile so that it reaches the surface of second sphere.
 11:15View Solution
11:15View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
07:00View Solutionसमान त्रिज्या R परन्तु M तथा 4M द्रव्यमान के दो एकसमान ठोस गोले इस प्रकार रखे हैं की इनके केंद्रों के बीच पृथकन (चित्र) 6R है। दोनों गोले स्थिर रखे गए हैं। M द्रव्यमान के किसी प्रक्षेप्य को M द्रव्यमान के गोले के पृष्ठ से 4M द्रव्यमान के गोले के केंद्र की ओर सीधे प्रक्षेप्य की उस न्यूनतम चाल के लिए व्यंजक प्राप्त कीजिए जिससे फेंके जाने पर वह दूसरे गोले के पृष्ठ पर पहुँच जाए ।
 View Solution
View Solutionसमान त्रिज्या R परन्तु द्रव्यमान M तथा 4M द्रव्यमान के दो एकसमान ठोस गोले इस प्रकार रखें हैं कि इनके केंद्रों के बीच पृथकन चित्र में दर्शाएं अनुसार 6R है। दोनों गोले स्थिर रखे गए हैं। m द्रव्यमान के किसी प्रक्षेप्य को M द्रव्यमान के गोले के पृष्ठ से 4M द्रव्यमान के गोले के केंद्र की ओर सीधे प्रक्षेपित किया जाता है। प्रक्षेप्य की उस न्यूतम चाल के लिए व्यंजक ज्ञात कीजिए जिससे फेंके जाने पर वह दूसरे गोले तक पहुँच जाए।
 View Solution
View SolutionTwo uniform solid spheres of equal radii R, but mass M and 4 M have a center to centre separation 6 R, as shown in figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
 View Solution
View SolutionTwo uniform solid spheres of equal radii R, but mass M and 4M have a centre to centre separation 6 R, the two spheres are held fixed on a horizontal floor. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. The minimum speed v of the projectile so that it reaches the surface of the second sphere:
View SolutionTwo uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown . The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
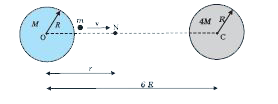 View Solution
View SolutionThe masses of two fixed sheres are M and 2M and the radius of each sphere is R. Their centres are 10R apart. The minimum speed with which a particle of mass M10 be projected from themid - point of the joining the centres of the two spheres so that it escapes to infinity is ..............
View SolutionTwo uniform solid spheres of equal radii R, but mass M and 4M have a centre to centre separation 6R, the two spheres are held fixed on a horizontal floor. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere
View SolutionTwo unifrom solid spheres of equal of radii R, but mass M and 4M have a centre to centre separation 6R, the two spheres are held fixed on a horizontal floor. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. The minimum speed v of the projectile so that it reaches the surface of the second sphere
04:18View SolutionTwo uniform solid spheres of equal radii R, but mass M and 4M have a centre to centre separation 6R, the two spheres are held fixed on a horizontal floor. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere
03:35View SolutionTwo unifrom solid spheres of equal of radii R, but mass M and 4M have a centre to centre separation 6R, the two spheres are held fixed on a horizontal floor. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. The minimum speed v of the projectile so that it reaches the surface of the second sphere
03:35View Solution

