Two uniform soild spheres of equal radii R but mass M and 4M have a centre to centre separation 6R, as shows in Fig. (a) The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of ten second. Obtain an expression for the minimum speed υ of the projectile so that it reaches the surface of second sphere.
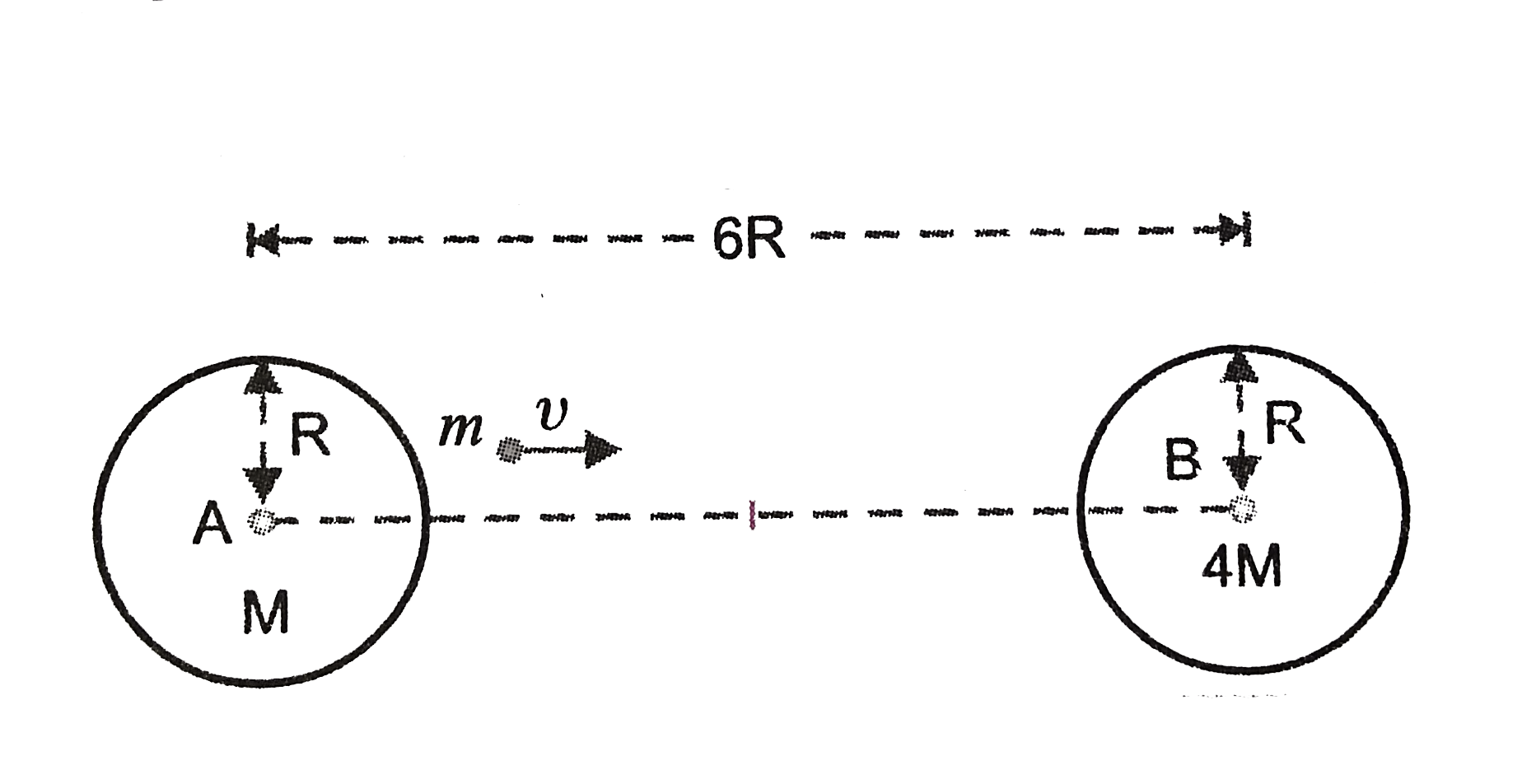
Refer to Fig. (b) let the projectile fired with minimum velocity υ from the surface of sphere A reach the surface of sphere B. Let C be the neutral point at a distance x from centre of sphere A where the gravitational pull on body due to sphere A is equal and opposite to the gravitational pull on body due to sphere B. Then
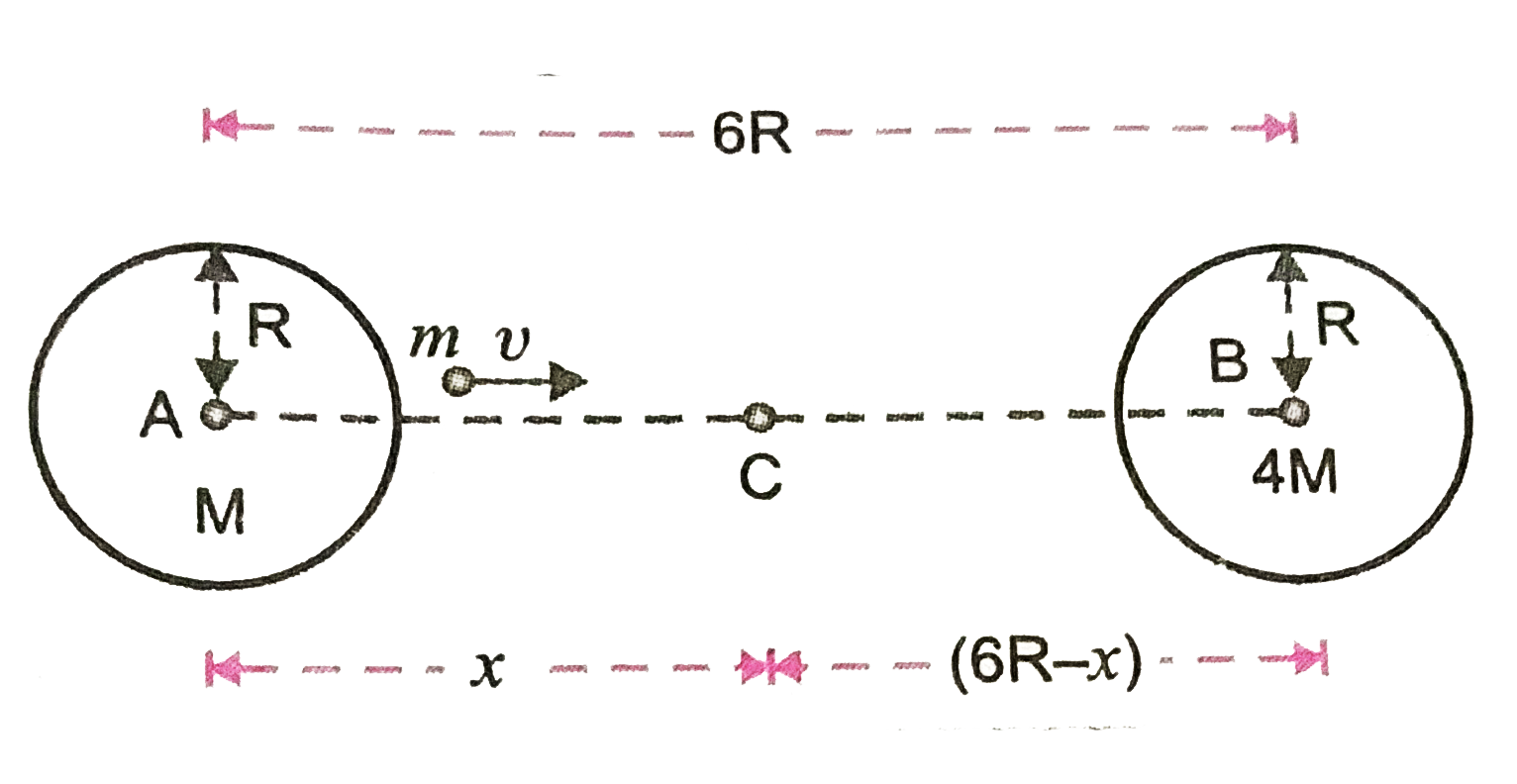
GMmx2=G4Mm(6R−x)2 or (6R−x)2=4x2
or 6R−x=±6R is not of any concern in this problem. Thus, AC=x=2R. Therefore, it is sufficient to project the particle with a minimum speed υ which enable it to each C Beyond that the greater gravitational pull of 4M will be suffficiently large to attract the projectile.
The mechanical energy of projectile at the surface of M is
Ei=12mυ2+(−GMmR)+(−G4Mm5R)
At the natural point C, the speed apporaches zero. The mechanical energy at C is purely potential . So
EC=−GMm2R−G4Mm4R
Using principle of conservation of mechanical energy
12mυ2−−GMmR−4GMm5R
=−GMm2R−4GMm4R
or υ2=2GMR[45−12]=3GM5R
or υ(3GM5R)1/2
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - SOLVED EXAMPLES TYPE H1videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - SOLVED EXAMPLES TYPE I1videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - SOLVED EXAMPLES TYPE G1videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Assertion - Reason Type questions14videos
BEHAVIOUR OF PERFECT GAS & KINETIC THEORY
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension4videos
KINEMATICS
Similar Questions
Two uniform solid spheres of equal radii R, but mass M. and 4M have a centre to centre separation 6R, as shown in the figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the center of the second sphere. If the minimum speed v of the projectile so that it reaches the surface of the second sphere is √xGMyR, then find (x,+y).
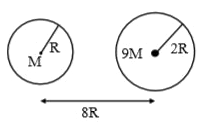
'(##CEN_KSR_PHY_JEE_C10_038_Q05##)'View SolutionSuppose two planets (spherical in shape) of radii R and 2R, but mass M and 9 M respectively have a centre to centre separation 8 R as shown in the figure. A satellite of mass 'm' is projected from the surface of the planet of mass 'M' directly towards the centre of the second planet. The minimum speed 'v' required for the satellite to reach the surface of the second planet is √a7GMR then the value of 'a' is ________.
[Given : The two planets are fixed in their position]
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two solid spherical planets of equal radii R having masses 4M and 9M their centre are separated by a distance 6R. A projectile of mass m is sent from theplanet of mass 4 M towards the heavier planet. What is the distance r of the point from the lighter planet where the gravitational force on the projectille is zero ?
A1.4 RB1.8 RC1.5 RD2.4 R - Question 2 - Select One
The gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
AGMa2BGMa3CGM2aDzero - Question 3 - Select One
Distance between the centres of two stars is 10a. The masses of these stars are M and 16M and their radii a and 2a respectively. A body of mass m is fired straight from the surface of the larger star towards the smaller star. The minimum initial speed for the body to reach the surface of smaller star is
A23√GmaB32√5GmaC23√5GmaD32√Gma
Two solid spherical planets of equal radii R have masses 4M and 9M. Their centres are scparated by a distance 6R. A projectile of mass m is sent from the planet of mass 4M towards the heavier planet. If the distance r of the point from the lighter planet where the gravitational 'force on the projectile is zero is kR, then calculate k.
View SolutionA particle of mass m is lying at the centre of a solid sphere of mass M and radius R. There is a turnel of negligible thickness, so that particle may escape. Find the minimum velocity required to escape the particle from the gravitational field of the sphere.
View SolutionIf a particle of mass 'm' is projected from a surface of bigger sphere of mass '16M' and radius '2a' then find out the minimum velocity of the particle such that the particle reaches the surface of the smaller sphere of mass M and radius 'a'. Given that the distance between the centres of two spheres is 10 a.
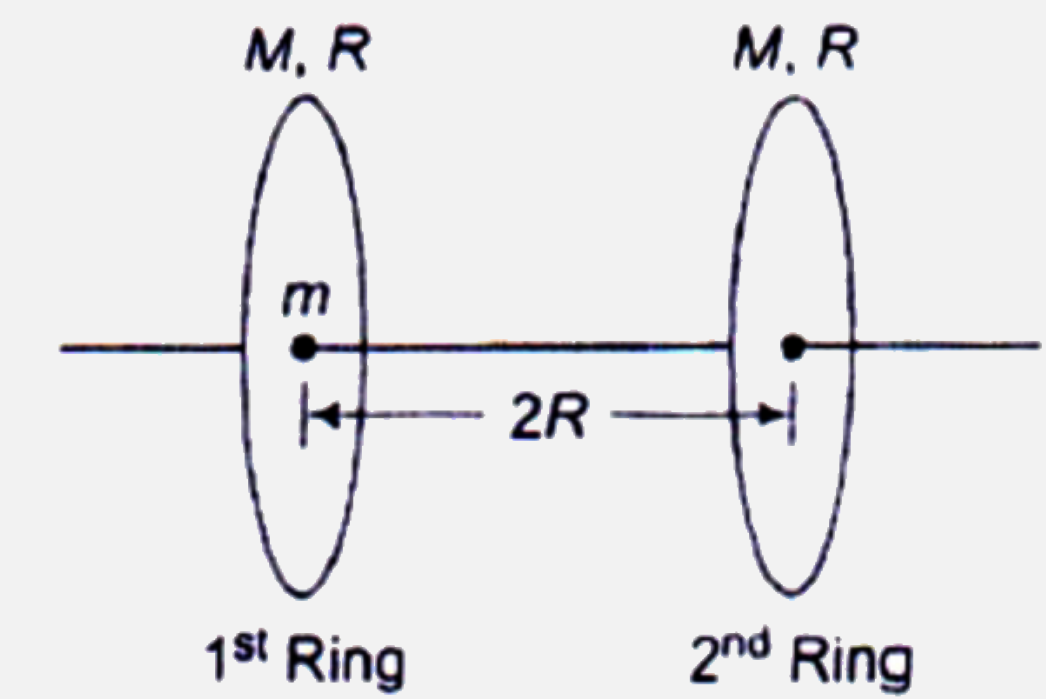
View SolutionConsider two identical rings of mass M and radius R fixed on a horizontal axis in a gravity - free space. A particle of mass m is held at rest at the centre of 1st ring and projected along the axis towards 2nd ring. The minimum speed of projection so that the particle reaches the centre of 2nd ring is
 View Solution
View SolutionA particle of mass m is located outside a uniform sphere of mass M at a distance r from its centre. Find:
(a) the potential energy of gravitational interaction of the particle and the sphere,
(b) the gravitational force which the sphere exerts on the particle.View Solution

