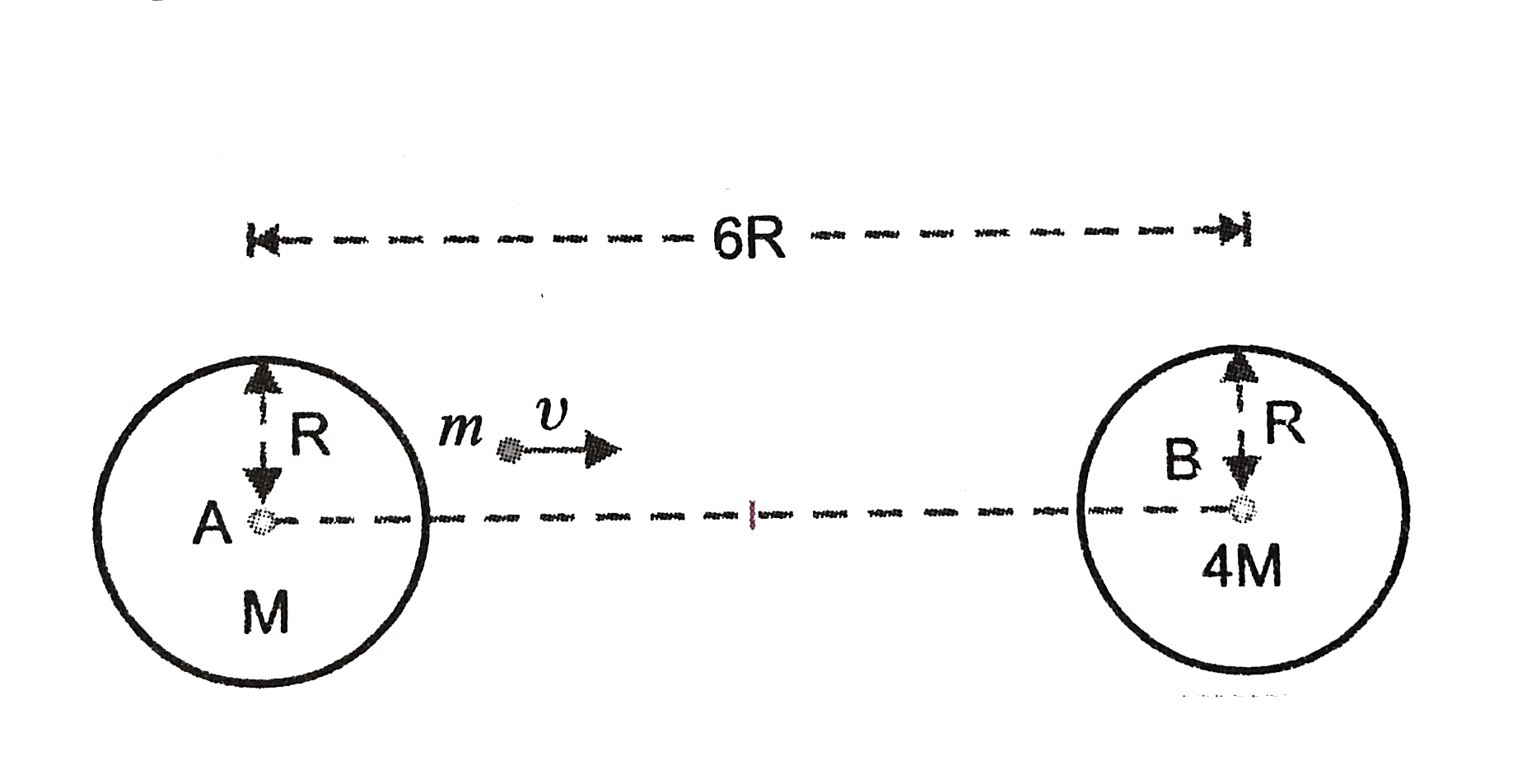
Two uniform solid spheres of equal radii R, but mass M and 4 M have a center to centre separation 6 R, as shown in figure. The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
 Solution in Gujrati
Solution in Gujrati
⇒ The gravitational force of spheres of mass M and 4M acted on the projectile body of mass m. Suppose, the resultant force on point N will be zero.
Suppose DN=r ∴NC=6R–r
Because, distance between centres of spheres is 6R.
The resultant force on point N is zero. ∴GMmr2=4GMm(6R−r)2
∴(6R−r)2=4r2
∴6R−r=2r or 6R−r=−2r
∴6R=3r ∴6R=−r
∴r=2R ∴r=−6R
The kinetic energy of body of mass m on the surface of mass MKi=12mv2
where velocity of body of mass m is v and potential energy
Ui=−GMmR−4GMm(6R−R)
=−GMmR−4GMm5R=9GMm5R
∴ Mechanical energy Ei=Ki+Ui
=12mv2mv2−9GMm5 ...(1)
Now at neutral point N, the velocity of projectile body is zero. Hence, mechanical energy at this point,
EN=−GMmr−4GMm(6R−r) [∴KN=0]
=GMm2r−4GMm4R [∴r=2R]
=−6GMm4R
∴EN=−3GMm2R ...(2)
From conservation of mechanical of mechanical energy,
Ei=EN
12mv2−9GMm5R=−3GMm2R
[∴ From equaiton (1) and (2)]
∴12mv2=9GMm5R−3GMm2R
=3GMm10R
∴v2=35GMR
∴v=√3GM5R
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - GRAVITATIONEXERCISE - Section - B Numerical From Textual Exercise (Answer the following:)21videos
GRAVITATION
- BOOK - KUMAR PRAKASHANCHAPTER - GRAVITATIONEXERCISE - Section - B ADDITIONAL EXERCISE4videos
GRAVITATION
- BOOK - KUMAR PRAKASHANCHAPTER - GRAVITATIONEXERCISE - Section - A Try Yourself (VSQs)76videos
GRAVITATION
- BOOK - KUMAR PRAKASHANCHAPTER - LAW OF MOTIONEXERCISE - (QUESTION PAPER) SECTION-D1videos
LAW OF MOTION
Similar Questions
You can shled a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means ?
13:19View SolutionAs you have learnt in the text a geostationary satellite orbits the earth at a height of nearly 36,000 km from the surface of the earth. What is the potential due to earth's gravity at the site of this satellite ? (Take the potential energy at infinity to be zero).
Mass of the earth 6.0×1024(kg) ,
Radius = 6400 km .07:04View SolutionDescribe Ptolemy model for planetary motion.
02:41View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
13:19View SolutionTwo uniform soild spheres of equal radii R but mass M and 4M have a centre to centre separation 6R, as shows in Fig. (a) The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of ten second. Obtain an expression for the minimum speed υ of the projectile so that it reaches the surface of second sphere.
 11:15View Solution
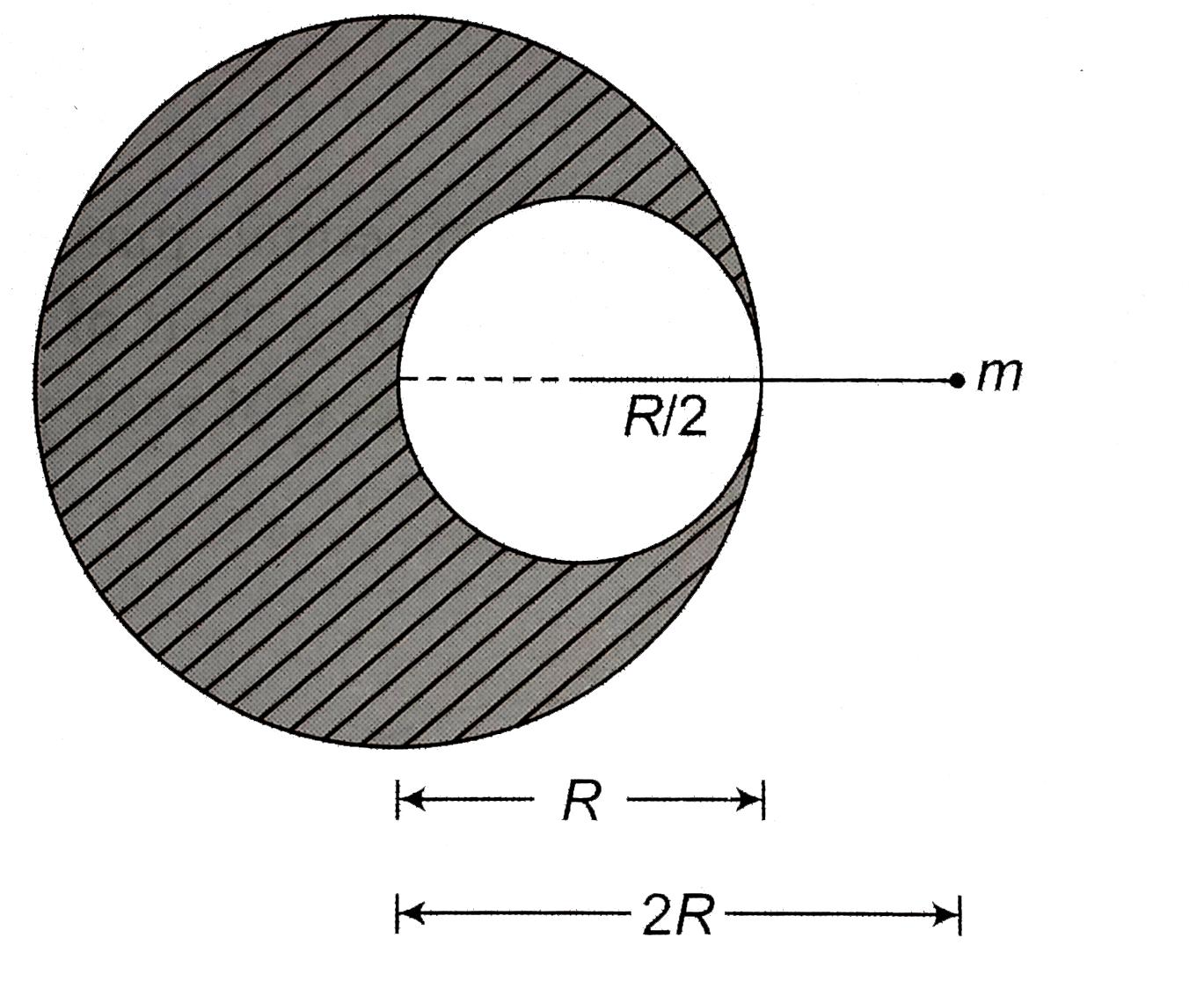
11:15View SolutionFrom a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown
 05:12View Solution
05:12View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View Solutionसमान त्रिज्या R परन्तु M तथा 4M द्रव्यमान के दो एकसमान ठोस गोले इस प्रकार रखे हैं की इनके केंद्रों के बीच पृथकन (चित्र) 6R है। दोनों गोले स्थिर रखे गए हैं। M द्रव्यमान के किसी प्रक्षेप्य को M द्रव्यमान के गोले के पृष्ठ से 4M द्रव्यमान के गोले के केंद्र की ओर सीधे प्रक्षेप्य की उस न्यूनतम चाल के लिए व्यंजक प्राप्त कीजिए जिससे फेंके जाने पर वह दूसरे गोले के पृष्ठ पर पहुँच जाए ।
 View Solution
View Solutionसमान त्रिज्या R परन्तु द्रव्यमान M तथा 4M द्रव्यमान के दो एकसमान ठोस गोले इस प्रकार रखें हैं कि इनके केंद्रों के बीच पृथकन चित्र में दर्शाएं अनुसार 6R है। दोनों गोले स्थिर रखे गए हैं। m द्रव्यमान के किसी प्रक्षेप्य को M द्रव्यमान के गोले के पृष्ठ से 4M द्रव्यमान के गोले के केंद्र की ओर सीधे प्रक्षेपित किया जाता है। प्रक्षेप्य की उस न्यूतम चाल के लिए व्यंजक ज्ञात कीजिए जिससे फेंके जाने पर वह दूसरे गोले तक पहुँच जाए।
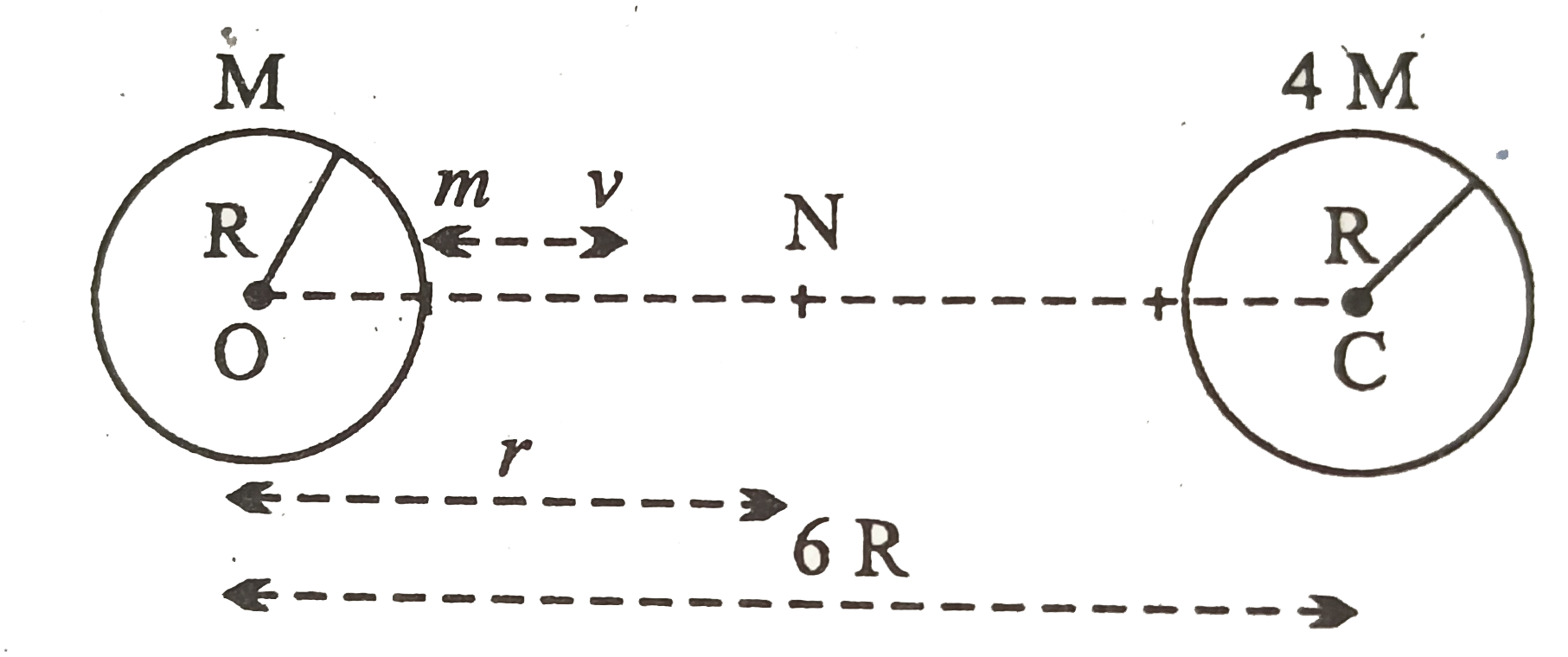 View Solution
View SolutionTwo uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown . The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
View SolutionTwo uniform solid spheres of equal radii R, but mass M and 4M have a centre to centre separation 6 R, the two spheres are held fixed on a horizontal floor. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. The minimum speed v of the projectile so that it reaches the surface of the second sphere:
View SolutionTwo uniform solid spheres of equal radii R, but mass M and 4 M have a centre to centre separation 6 R, as shown . The two spheres are held fixed. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere.
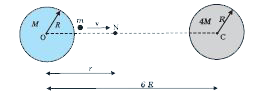 View Solution
View SolutionTwo uniform solid spheres of equal radii R, but mass M and 4M have a centre to centre separation 6R, the two spheres are held fixed on a horizontal floor. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere
04:18View SolutionTwo unifrom solid spheres of equal of radii R, but mass M and 4M have a centre to centre separation 6R, the two spheres are held fixed on a horizontal floor. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. The minimum speed v of the projectile so that it reaches the surface of the second sphere
01:57View SolutionTwo uniform solid spheres of equal radii R, but mass M and 4M have a centre to centre separation 6R, the two spheres are held fixed on a horizontal floor. A projectile of mass m is projected from the surface of the sphere of mass M directly towards the centre of the second sphere. Obtain an expression for the minimum speed v of the projectile so that it reaches the surface of the second sphere
04:56View Solution

