(a) Define electric flux. Write its S.I. units.
(b) Using Gauss's law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
(c ) How is the field directed if (i) the sheet is positively charged, (ii) negatively charged ?

Text Solution

Verified by Experts

(a) Electric flux is defined as the dot product of electric field intensity vector. Its S.I. unit is $N m^{2} / C$ .
(b) Let $σ$ be the uniform surface charge density of an infinite plane sheet. Consider a Gaussian surface to be a rectangular sectional area A.

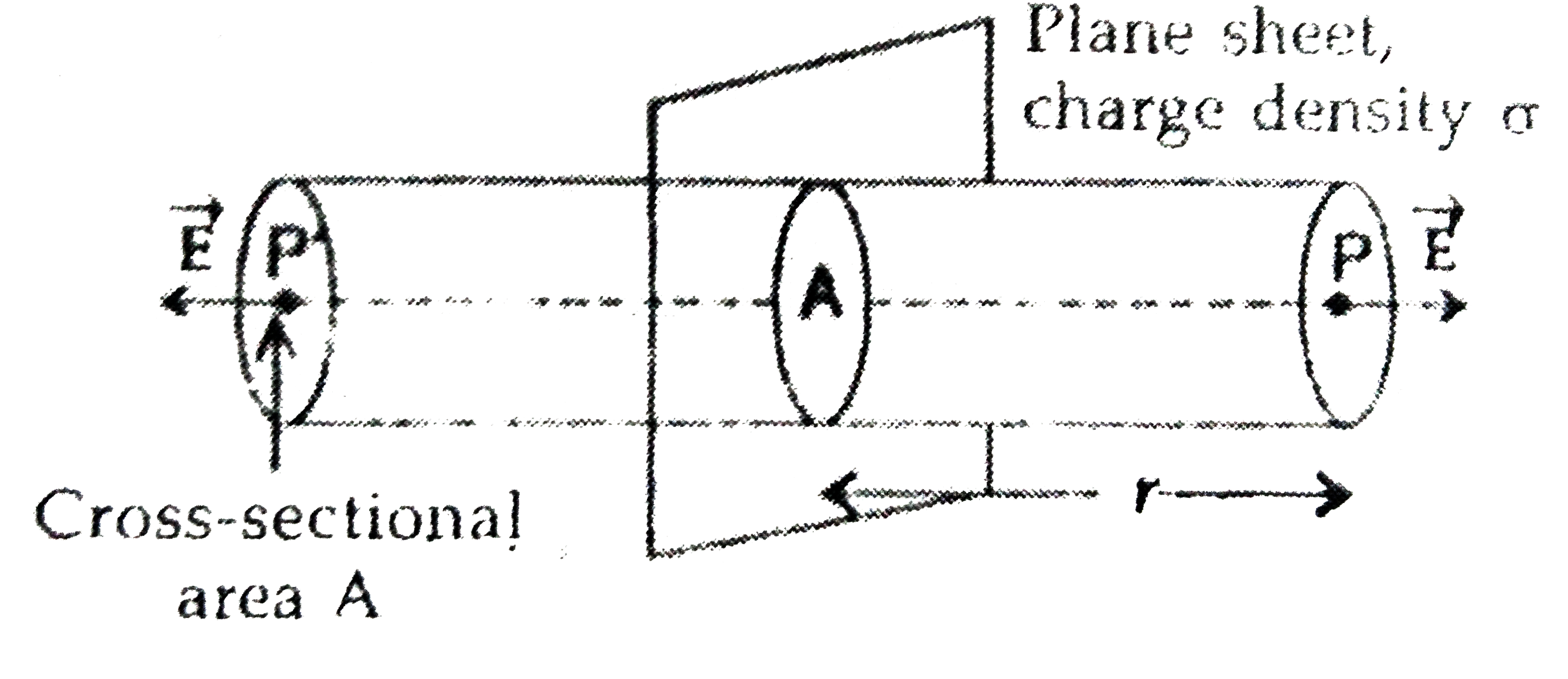
From figure, only the two faces 1 and 2 will contribute to flux. Electric field lines are parallel to the other faces and they do not contribute to the total flux.
The net flux through the Gaussian surface is 2EA. The charge enclosed by the closed surface is $σ A$ .
By Gauss's law, $2 E A = \frac{σ A}{\in_{0}} or \to E = \frac{σ}{2 \in_{0}} ˆ n$
Since the expression does not contain x, so electric field is independent of the distance.
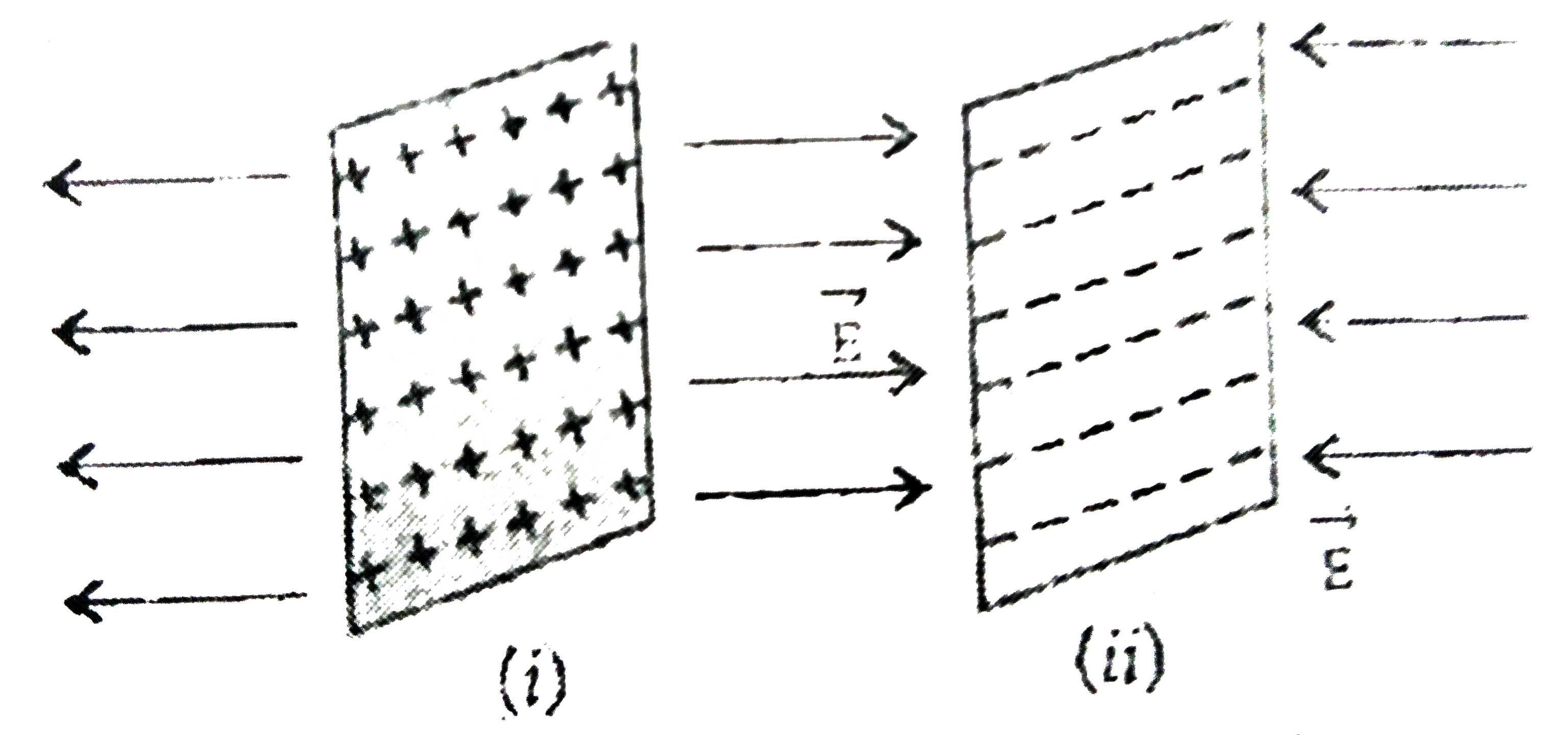
(c ) (i) The electric field is directed perpendicularly away from the sheet.
(ii) The electric field is directed perpendicularly towards the sheet.

Updated on:21/07/2023

The expression for electric field intensity at a points outside uniformly charged thin plane sheet is (where, d is the distance of point from plane sheet)
Aindependent of d
Bdirectly proportional to $\sqrt{d}$
Cdirectly proportional to d
Ddirectly proportional to $\frac{1}{\sqrt{d}}$
The intensity of electric field at a point due to charged conductor of any shape or plane charged sheet is
Aindependent of distance of that point
Bdepends on distance of that point
Cindependent of charge density and surrounding medium
Dnone of these