Question

Using Gauss' law porve that the electric field at a point due to a uniformaly charged infinite plane sheet is independent of the distance form it. How is the field directed if the sheet is
(i) positively charged, (ii) negatively charged.

Explanation

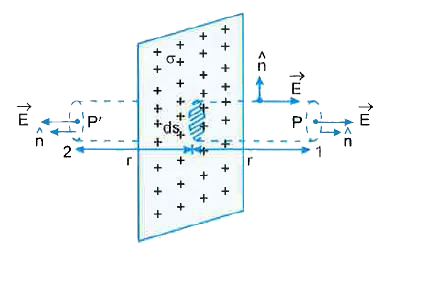
For Gauss. theorem , see point number 47 under the heading "Chapter At A Glance" Consider an infinite thin plane sheet having a surface density ` sigma. ` To find electric field at a point P situated at a normal distance r from the sheet , consider an imaginary cylinder of cross-section ara ds around point P and length 2r, passing through the sheet ,as the Gaussian surface.
From symmetry consideration , only side faces1 and 2 of cylinder contribute towards the flux because here
` oversetto E and hatn ` parallel but the curved surface of cylinder does not contributed towards the flux because here `oversetto E and hatn ` are mutually perpendicular.
` therefore ` Total electric flux ` phi_in =2 E ds`
As per Gauss theorem total electric flux `pi_in =(1)/( in_0) ` (charge encloesd) `=(1)/( in _0) .(sigma ds) `
Comparing (i) and (ii) , we get
` 2 E ds =(sigma)/( in_0) . ds rArr E= ( sigma)/( 2 in _0) `
Thus, the electric field at a point due to a uniformaly charged infinite plane sheet is independent of the distance from it .
Vectorially ` oversetto (E) =(sigma)/(2 in _0) hatr `
Thus for (i) positively charged sheet electric field `oversetto E ` is directed outwards and for (ii) negatively charged sheet the field is directed inwards.