(a) Define the term 'conductivity' of a metallic wire. Write its SI unit.
(b) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in te'rms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E.
(a) The resistivity and conductivity are proportionally constant and, therefore, depend only on the material the wire is made of not the geometry of wire.
The reciprocal of resistivity of the material of a conductor is called conductivity.
S.I unit = mho - m−1/ siemen m−1.
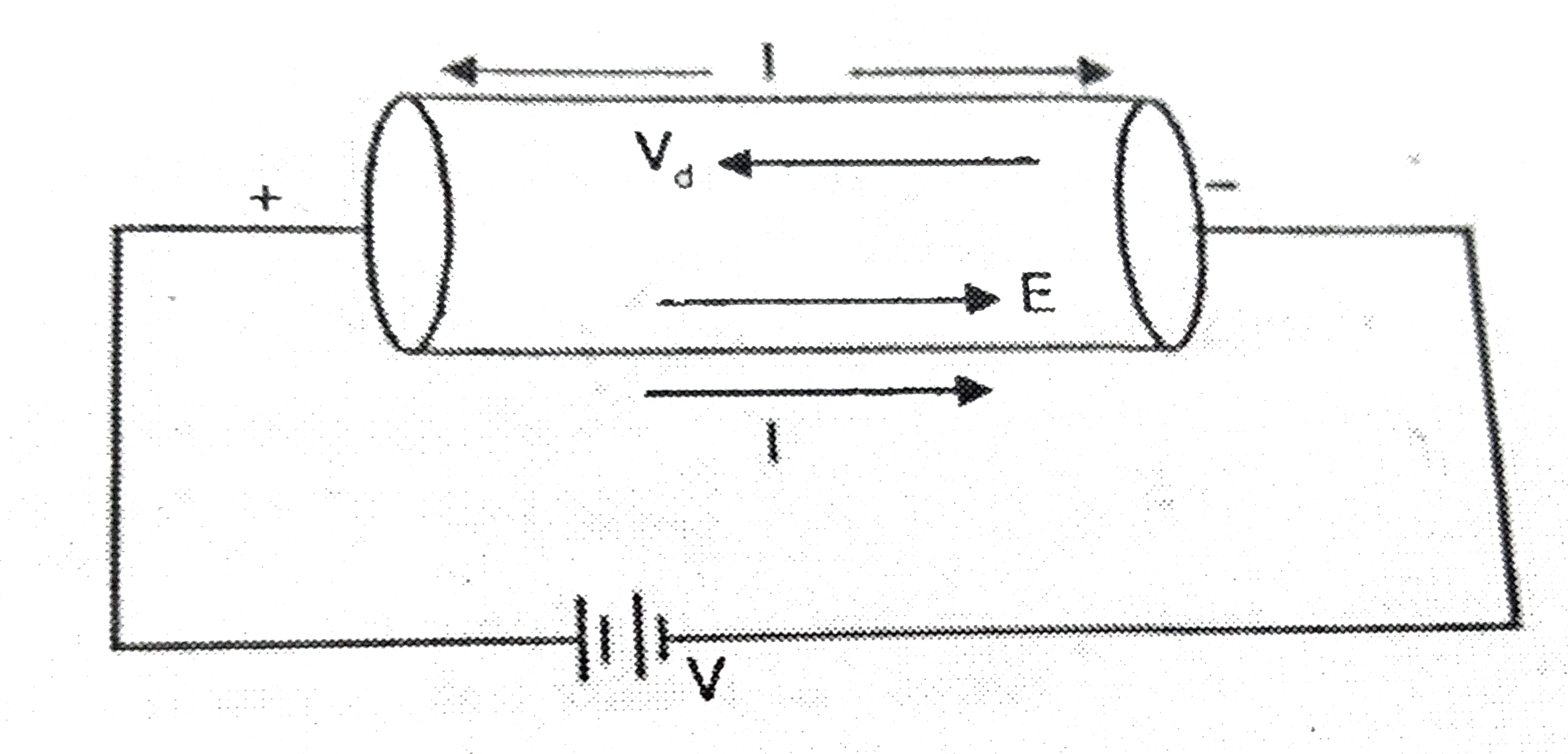
(b) Let us consider a wire of length l and cross-sectional area A. When potential V is applied at the terminals of wire then electric field F. generate inside the conductor and all the e−1 flow towards the+ ve terminal of bett'ery with drift velocity Vd.
Let the conductor no. of e−1 per units.
Volue is n then no. of e− in it .
= Volume of wire ×e−1 density = area × lenght Xn = Aln.
If charge of each electron ,is e, then total frequency charge q = nAle
If the time taken by the electrons to cover the distance l is =
Detla=l/Vd
Floing current i=qΔt
i=nA≤l/Vd=nAeVd
We know that current density
J = (i)/(A) = (cancel(nAe)V_(d))/(cancel(A))
J=neVd
Drift volocity Vd=(eEτm)
Where, τ= Relaxtion time
Then, J=≠(eEτm)
J=≠2τFm
J=σE where σ=ne2τm.
Topper's Solved these Questions
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION - A7videos
XII BOARDS
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION - B9videos
XII BOARDS
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTION - E6videos
XII BOARDS
- BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
Define the term electrical conductivity of a metallic wire. Write its SI unit.
View SolutionDefine electrical conductivity of a metallic wire. Write its SI unit.
View SolutionDefine the term electrical conductivity of a metallic wire. Write its SI unit.
View SolutionDefine the term electrical conductivity of a metallic wire. Write its SI unit.
View SolutionDefine drift velocity of free electron . If relaxation time is r then write a vector relation b etween drift velocity and electric field.
View SolutionDefine drift velocity of free electron . If relaxation time is r then write a vector relation b etween drift velocity and electric field.
View SolutionDerive the expression for drift velocity of free electron in terms of relaxation time and electric field applied across a conductor.
View SolutionDerive the expression for drift velocity of free electron in terms of relaxation time and electric field applied across a conductor.
View SolutionDerive the expression for drift velocity of free electron in terms of relaxation time and electric field applied across a conductor.
View SolutionDerive the expression from drift velocity of free electron in terms of relaxation time and electric field applied across a conductor.
View Solution

