A particle starts from point A moves along a straight line path with an aceleration given by a=p-qx where p,q are constants and x is distance from point A. The particle stops at point B. The maximum velocity of the paticle is

$\frac{p}{q}$

$\frac{p}{\sqrt{q}}$

$\frac{q}{p}$

$\frac{\sqrt{q}}{p}$

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

A particle starts from point A moves along a straight line path with an acceleration given by $a = p - q x$ where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
A $\frac{p}{q}$
B $\frac{p}{\sqrt{q}}$
C $\frac{q}{p}$
D $\sqrt{\frac{q}{p}}$
A particle starts from point A moves along a straight line path with an acceleration given by a = p - qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
A $\frac{p}{q}$
B $\frac{p}{\sqrt{q}}$
C $\frac{q}{p}$
D $\sqrt{\frac{q}{p}}$
A particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
A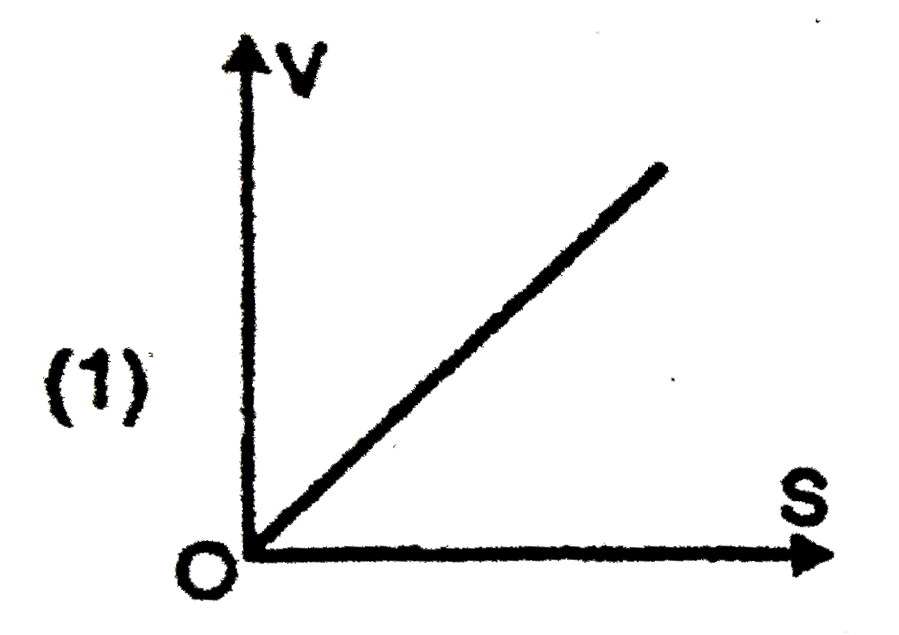
B
C
D