Derive the relation R=R1+R2+R3. When resistors are joined in series.
In series combination, the same current flows in all the resistances but the potential difference across each of the resistance is different.
According to Ohm law , we have
V1=IR1,V2=IR2,V3=IR3
IF the total potential difference between A and B is V, then
V=V1+V2+V3
=IR1+IR2+IR3=I(R1+R2+R3)
Let the equivalent resistance be R, then
V=IR
and hence IR=I(R1+R2+R3)
⇒R=R1+R2+R3

Topper's Solved these Questions
- ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - ELECTRICITY EXERCISE - LONG ANSWER QUESTION
18 Videos
- ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - ELECTRICITY EXERCISE - VERY SHORT ANSWER QUESTIONS
54 Videos
- CBSE SAMPLE QUESTION PAPER 2019 - 20 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE SAMPLE QUESTION PAPER 2019 - 20 (SOLVED)EXERCISE - SECTION A
10 Videos
- LIGHT - REFLECTION AND REFRACTION BOOK - U-LIKE SERIESCHAPTER - LIGHT - REFLECTION AND REFRACTION EXERCISE - LONG ANSWER QUESTIONS
14 Videos
Similar Questions
Derive the relation 1R=1R1+1R2+1R3 when resistors are joined in parallel.
View SolutionFor the series combination of three resistors establish the relation :
R=R1+R2+R3
where the symbols have their usual meanings.
Calculate the equivalent resistance of the combination of three resistors of 6Ω,9Ω and 18Ω joined in parallel.
View Solution
Knowledge Check
In an electric circuit three resistors R1,R2andR3 are connected in series such that R2=R3. IF V1,V2andV3 are the voltage across R1,R2andR3 respectively , then
AV1=V2BV2=V3CV1=V3DV1=V2=V3Assertion (A): In series grouping of resistances the equivalent resistance is greater than even the biggest resistance joined in series.
Reason (R ): In series arrangement the equivalent resistance Rs is given as per the relation 1R=1R1+1R2+1R3+......ABoth (A) and (R ) are true and (R ) is correct explanation of the assertionBBoth (A ) and ( R) are true but (R ) is not the correct explanation of the assertion.C(A ) is true but (R ) is falseD(A) is false but (R ) is trueThree resistors having values R1,R2andR3 are connected in series to a battery.Suppose R1 carries a current of 2.0 A,R2 has resistance of 3.0 ohms, and R3 dissipates. 6.0 watts of power. Then the voltage across R3 is
A1 VB2 VC3 VD4 V
For the series combination of three resistors establish the relation :
R=R1+R2+R3
where the symbols have their usual meanings.
Calculate the equivalent resistance of the combination of three resistors of 6Ω,9Ω and 18Ω joined in parallel.
View SolutionWrite the expressions for the equivalent resistance R of three resistors R1,R2,andR3 joined in (a) parallel, and (b) series.
View SolutionFind out the relation between R1,R2,R3andR4.so there is no that current in R.
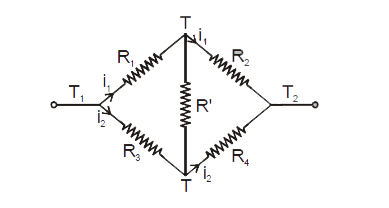
View SolutionThree resistors having values R1,R2andR3 are connected in series to a battery.Suppose R1 carries a current of 2.0 A,R2 has resistance of 3.0 ohms, and R3 dissipates. 6.0 watts of power. Then the voltage across R3 is
View SolutionThree resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
IfR_(1), R_(2)and R,_(3)are put in series, the effective resistance will be
View Solution
