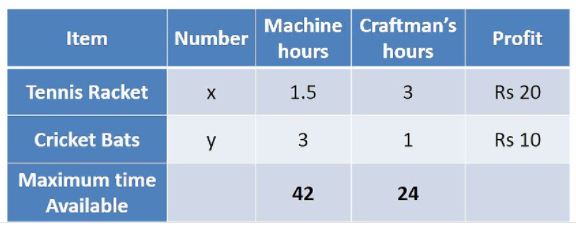
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftmans time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftmans time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmans time. If the profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the number of tennis rackets and crickets bats that the factory must manufacture to earn the maximum profit. Make it as an L.P.P. and solve graphically.
Let Number of Tennis Racket be x, and
Number of Cricket Bats be y
According to question:
Machine Hours
Tennis Racket requires → 1.5 hrs
Cricket Bat requires → 3 hrs
Maximum time available →42 hrs
∴
1.5x+3y≤42
3x+6y≤84
x+2y≤28
Craftsman's Hours
Tennis Racket requires → 3 hrs
Cricket Bat requires → 1 hrs
Maximum time available →24 hrs
∴
3x+y≤24
Also, x≥0,y≥0
As we want to maximize the profit.
Hence, the function used here will be Maximize Z
Profit on each tennis racket → Rs 20
Profit on each cricket Bat → Rs 10
∴
Maximize Z=20x+10y
Subject to constraints,
x+2y≤28
3x+y≤24
x≥0,y≥0

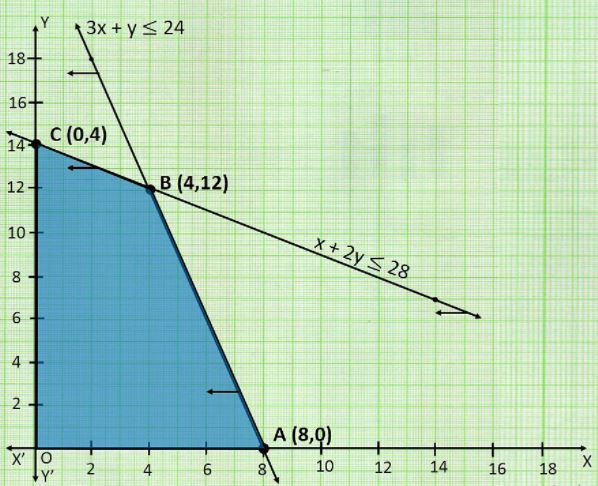
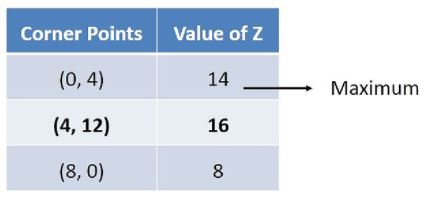
Thus,
(i) 4 Tennis Rackets and 12 Cricket Bats must be made so that factory runs at full capacity.
(ii) Maximum Profit is Rs 200, when 4 tennis rackets and 2 cricket bats are produced.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NCERT ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - SOLVED EXAMPLES
11 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERT ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Solved Examples
13 Videos
- MATRICESBOOK - NCERT ENGLISHCHAPTER - MATRICESEXERCISE - All Questions
105 Videos
Similar Questions
A cottage industry manufactures pedestal lamps and wooden shades.Both the products require machine time as well as craftsman time in the making. The number of hours required for producing 1unit of each and the corresponding profit is given in the following table : In a day, the factory has availability of not more than 42 hours of machine time and 24 hours of craftsman time, Assuming that all items manufactured manufacturer schedule his daily production in order to maximize profit ? Formulate it as an LPP and solve it graphically.

View SolutionA cottage industry manufactures pedestal lamps and wooden shades.Both the products require machine time as well as craftsman time in the making.The number of hours required for producing 1 unit of each and the corresponding profit is given in the following table:
In a day,the factory has availability of not more than 42 hours of machine time and 24 hours of craftsman time.
Assuming that all items manufactured are sold,how should the manufacturer schedule his daily production in order to maximise the profit?Formulate it as an LPP and solve it graphically
View SolutionFind the fractions:
5 hours of a day
View SolutionFind the ratio of 1 hour to 12 hours.
View SolutionDifference between 12-hour clock and 24-hour clock
View SolutionA manufacturer produces two types of steel trunks. He has tow machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 and Rs. 25 per trunk of the first type and the second respectively. How many trunks of each type must he make each day to makes maximum profit?
View SolutionA manufacturer produces nuts and bolts. It takes 2 hours work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 2 hours on machine B to produce a package of bolts. He earns a profit of Rs. 24 per package on nuts and Rs. 18 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 10 hours a day. Make an L.P.P. from above and solve it graphically ?
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes one hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade is Rs. 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit? Make an L.P.P. and solve it graphically.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes one hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade is Rs. 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit? Make an L.P.P. and solve it graphically.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 25 and that from a shade is Rs. 15. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit. Formulate an LPP and solve it graphically.
View Solution
