Question

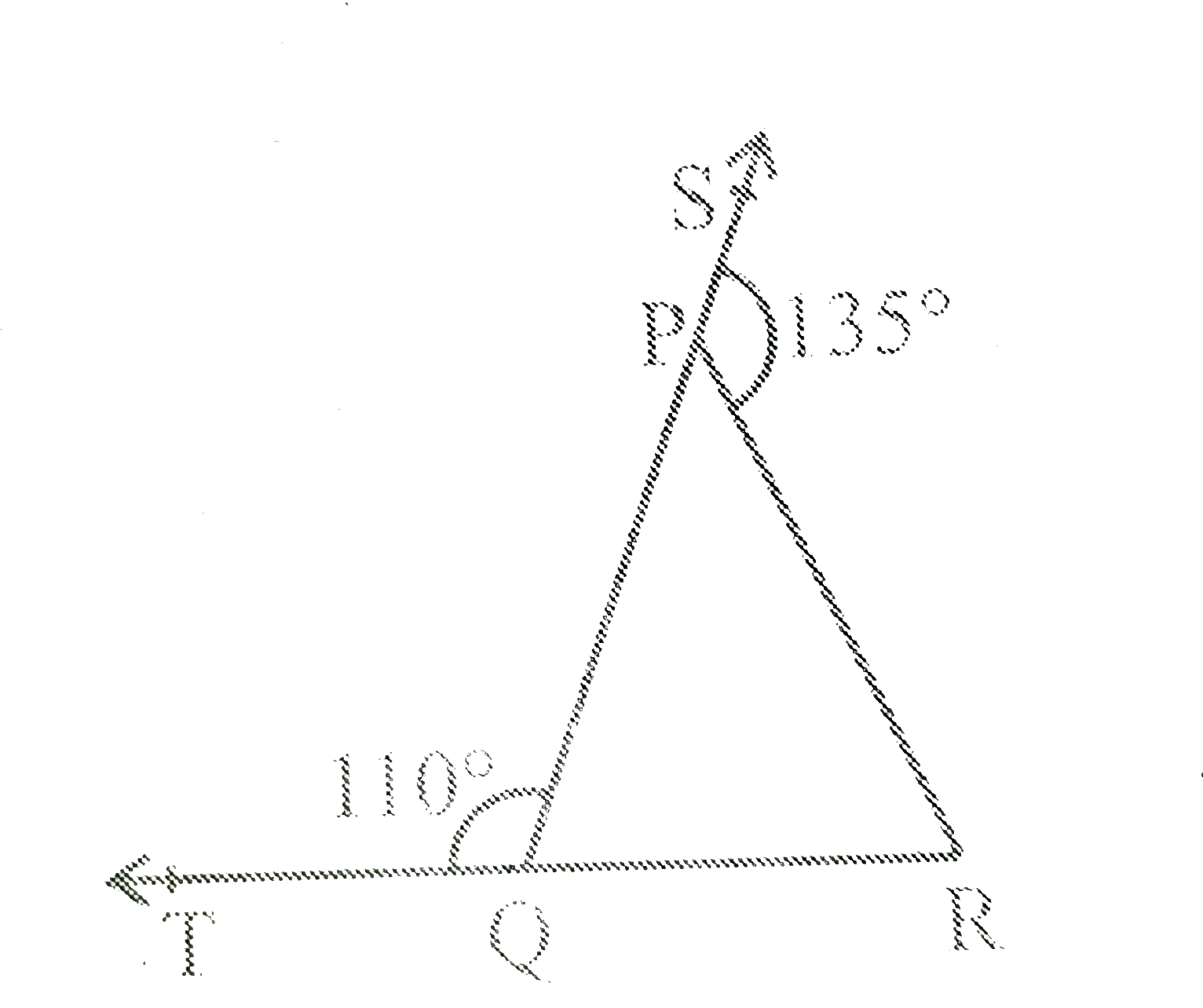
In figure, sides $QP$
and $RQ$
of $PQR$
are produced to point $S$
and $T$
respectively. If $\angle SPR={135}^0$
and $\angle PQT={110}^0,$
find $\angle PRQ\stackrel{.}{}$

Figure

Explanation

To solve the problem step by step, we will follow the reasoning provided in the video transcript and use the properties of triangles and angles.

Step 1: Draw the Diagram
We start by drawing triangle \( PQR \). Extend the sides \( QP \) to point \( S \) and \( RQ \) to point \( T \). Label the angles as follows:
- \( \angle SPR = 135^\circ \)
- \( \angle PQT = 110^\circ \)

Step 2: Identify Angles in Triangle
In triangle \( PQR \):
- Let \( \angle PRQ = A \)
- Let \( \angle PQR = B \)
- Let \( \angle QRP = C \)

According to the properties of triangles:
\( A + B + C = 180^\circ \quad \text{(Equation 1)} \)

Step 3: Use Exterior Angle Theorem
The exterior angle theorem states that an exterior angle of a triangle is equal to the sum of the two opposite interior angles. Thus, we can write:
1. For \( \angle SPR \):
\( A + C = 135^\circ \quad \text{(Equation 2)} \)
2. For \( \angle PQT \):
\( B + C = 110^\circ \quad \text{(Equation 3)} \)

Step 4: Add Equations 2 and 3
Now, we add Equation 2 and Equation 3:
\( (A + C) + (B + C) = 135^\circ + 110^\circ \)
This simplifies to:
\( A + B + 2C = 245^\circ \quad \text{(Equation 4)} \)

Step 5: Subtract Equation 1 from Equation 4
Now, we subtract Equation 1 from Equation 4:
\( (A + B + 2C) - (A + B) = 245^\circ - 180^\circ \)
This simplifies to:
\( 2C = 65^\circ \)
Dividing both sides by 2 gives:
\( C = 32.5^\circ \)

Step 6: Find Angle \( C \)
We can now substitute \( C \) back into either Equation 2 or Equation 3 to find \( A \) or \( B \). Let's use Equation 2:
\( A + 32.5^\circ = 135^\circ \)
Thus,
\( A = 135^\circ - 32.5^\circ = 102.5^\circ \)

Step 7: Find Angle \( B \)
Using Equation 3:
\( B + 32.5^\circ = 110^\circ \)
Thus,
\( B = 110^\circ - 32.5^\circ = 77.5^\circ \)

Final Answer
Thus, the angles in triangle \( PQR \) are:
- \( A = 102.5^\circ \)
- \( B = 77.5^\circ \)
- \( C = 32.5^\circ \)

The angle \( \angle PRQ \) is \( 32.5^\circ \).