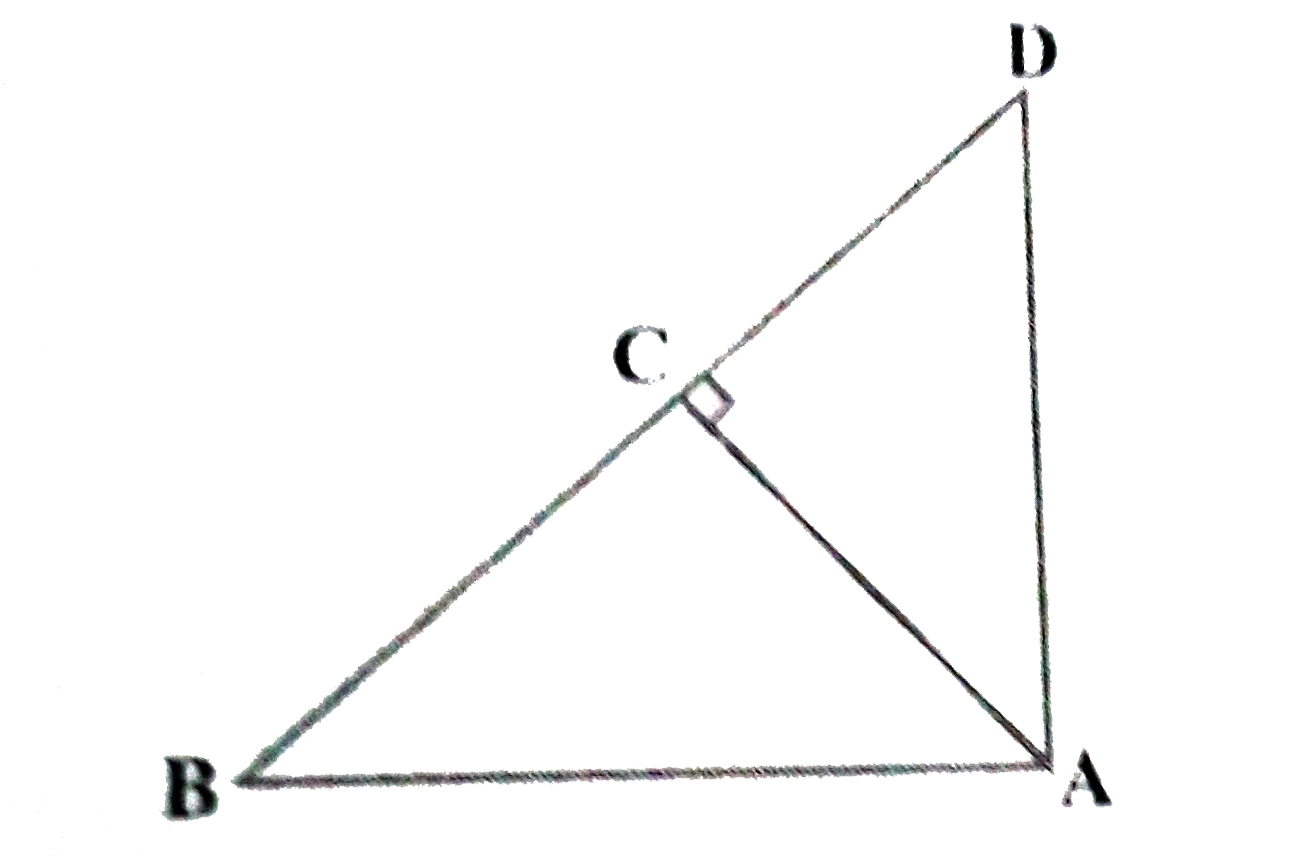
ABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
To solve the problem step by step, we will prove each of the four statements one by one using the properties of similar triangles.
Given:
- Triangle ABD is a right triangle, right-angled at A.
- AC⊥BD.
To Prove:
1. AB2=BC⋅BD
2. AC2=BC⋅CD
3. AD2=BD⋅CD
4. AB2AC2=BDDC
Step 1: Proving AB2=BC⋅BD
1. Identify Similar Triangles:
- In triangles BCA and BAD, we have:
- ∠BCA=90∘ (right angle)
- ∠BAD=90∘ (right angle)
- ∠ABC is common to both triangles.
- Therefore, by the Angle-Angle (AA) similarity criterion, △BCA∼△BAD.
2. Set Up Ratios:
- From the similarity, we have:
BCAB=ACAD=ABBD
3. Cross Multiply:
- From BCAB=ABBD, we cross-multiply:
BC⋅BD=AB2
4. Conclusion:
- Thus, we have proved:
AB2=BC⋅BD
- Triangle ABD is a right triangle, right-angled at A.
- AC⊥BD.
1. AB2=BC⋅BD
2. AC2=BC⋅CD
3. AD2=BD⋅CD
4. AB2AC2=BDDC
- In triangles BCA and BAD, we have:
- ∠BCA=90∘ (right angle)
- ∠BAD=90∘ (right angle)
- ∠ABC is common to both triangles.
- Therefore, by the Angle-Angle (AA) similarity criterion, △BCA∼△BAD.
- From the similarity, we have:
BCAB=ACAD=ABBD
- From BCAB=ABBD, we cross-multiply:
BC⋅BD=AB2
- Thus, we have proved:
AB2=BC⋅BD
Topper's Solved these Questions
Similar Questions
In Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
View SolutionABC is a right triangle right-angled at A and AD⊥BC . Then, BDDC= mm (a) (ABAC)2 (b) ABAC (c) (ABAD)2 (d) ABAD
View SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
View SolutionIn Figure, ABC is an obtuse triangle, obtuse angled at B . If AD⊥CB , prove that AC2=AB2+BC2+2 BC×BD .
View SolutionD is a point on the side BC of a triangle ABC such that ∠ADC=∠BAC. Show that CA2=CB.CD.
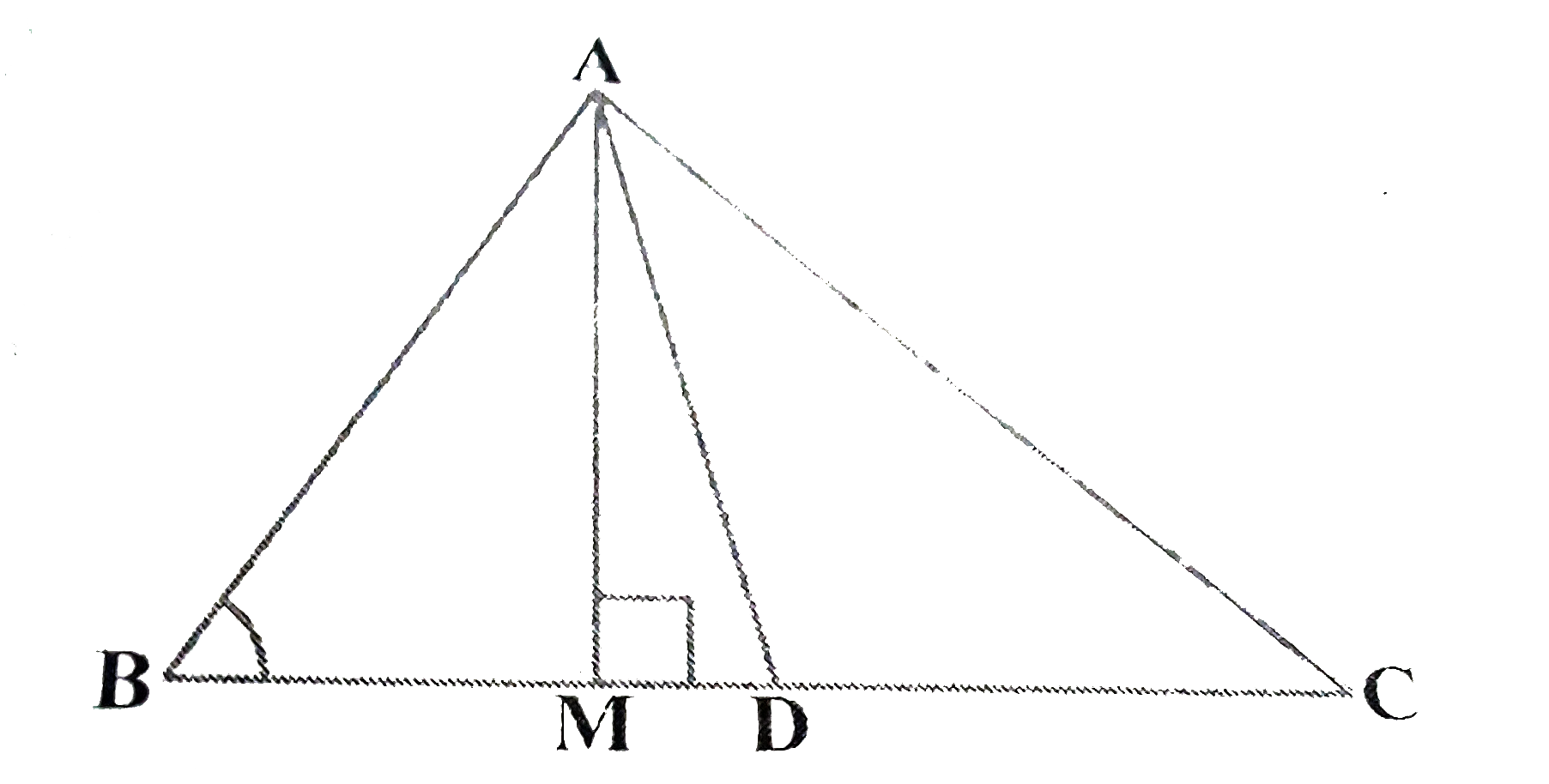
View SolutionIn figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn Figure, ∠ACB=90. and CD⊥AB . Prove that CB2CA2=BDAD
View SolutionIn a right ABC right-angled at C , if D is the mid-point of BC , prove that BC2=4 (AD2−AC2) .
View SolutionIn figure ∠ACB=90∘and CD⊥AB. Prove that BC2AC2=BDAD.
View Solution
