A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60∘. Find the length of the string, assuming that there is no slack in the string.
To solve the problem step by step, we will use trigonometric ratios.
Step 1: Understand the scenario
We have a kite flying at a height of 60 m above the ground, and the string makes an angle of 60° with the ground. We need to find the length of the string (let's denote it as AC).
Step 2: Identify the right triangle
In this scenario, we can visualize a right triangle where:
- The height of the kite (60 m) is the opposite side (AB).
- The length of the string (AC) is the hypotenuse.
- The horizontal distance from the point on the ground to the point directly below the kite is the adjacent side (BC).
Step 3: Use the sine function
We can use the sine function, which relates the angle of inclination to the opposite side and the hypotenuse:
sin(θ)=OppositeHypotenuse
Here, θ=60∘, the opposite side is 60 m (height of the kite), and the hypotenuse is AC (length of the string).
Step 4: Substitute the values into the sine function
sin(60∘)=60AC
We know that sin(60∘)=√32. Therefore, we can write:
√32=60AC
Step 5: Cross-multiply to solve for AC
Cross-multiplying gives us:
√3⋅AC=120
Now, divide both sides by √3:
AC=120√3
Step 6: Rationalize the denominator
To rationalize the denominator, multiply the numerator and the denominator by √3:
AC=120⋅√3√3⋅√3=120√33
This simplifies to:
AC=40√3
Final Answer
The length of the string is 40√3 meters.
---
We have a kite flying at a height of 60 m above the ground, and the string makes an angle of 60° with the ground. We need to find the length of the string (let's denote it as AC).
In this scenario, we can visualize a right triangle where:
- The height of the kite (60 m) is the opposite side (AB).
- The length of the string (AC) is the hypotenuse.
- The horizontal distance from the point on the ground to the point directly below the kite is the adjacent side (BC).
We can use the sine function, which relates the angle of inclination to the opposite side and the hypotenuse:
sin(θ)=OppositeHypotenuse
Here, θ=60∘, the opposite side is 60 m (height of the kite), and the hypotenuse is AC (length of the string).
sin(60∘)=60AC
We know that sin(60∘)=√32. Therefore, we can write:
√32=60AC
Cross-multiplying gives us:
√3⋅AC=120
Now, divide both sides by √3:
AC=120√3
To rationalize the denominator, multiply the numerator and the denominator by √3:
AC=120⋅√3√3⋅√3=120√33
This simplifies to:
AC=40√3
The length of the string is 40√3 meters.
Topper's Solved these Questions
Similar Questions
The string of a kite is 100 metres long and it makes an angle of 60o with the horizontal. Find the height of the kite, assuming that there is no slack in the string.
View SolutionA kite is flying at a height of 75 metres from the ground level, attached to a string inclined at 60∘ to the horizontal. Find the length of the string to the nearest metre.
View SolutionThe length of a string between a kite and a point on the ground is 90 metres. If the string makes an angle θ with the ground level such that tanθ=158, how high is the kite? Assume that there is no slack in the string.
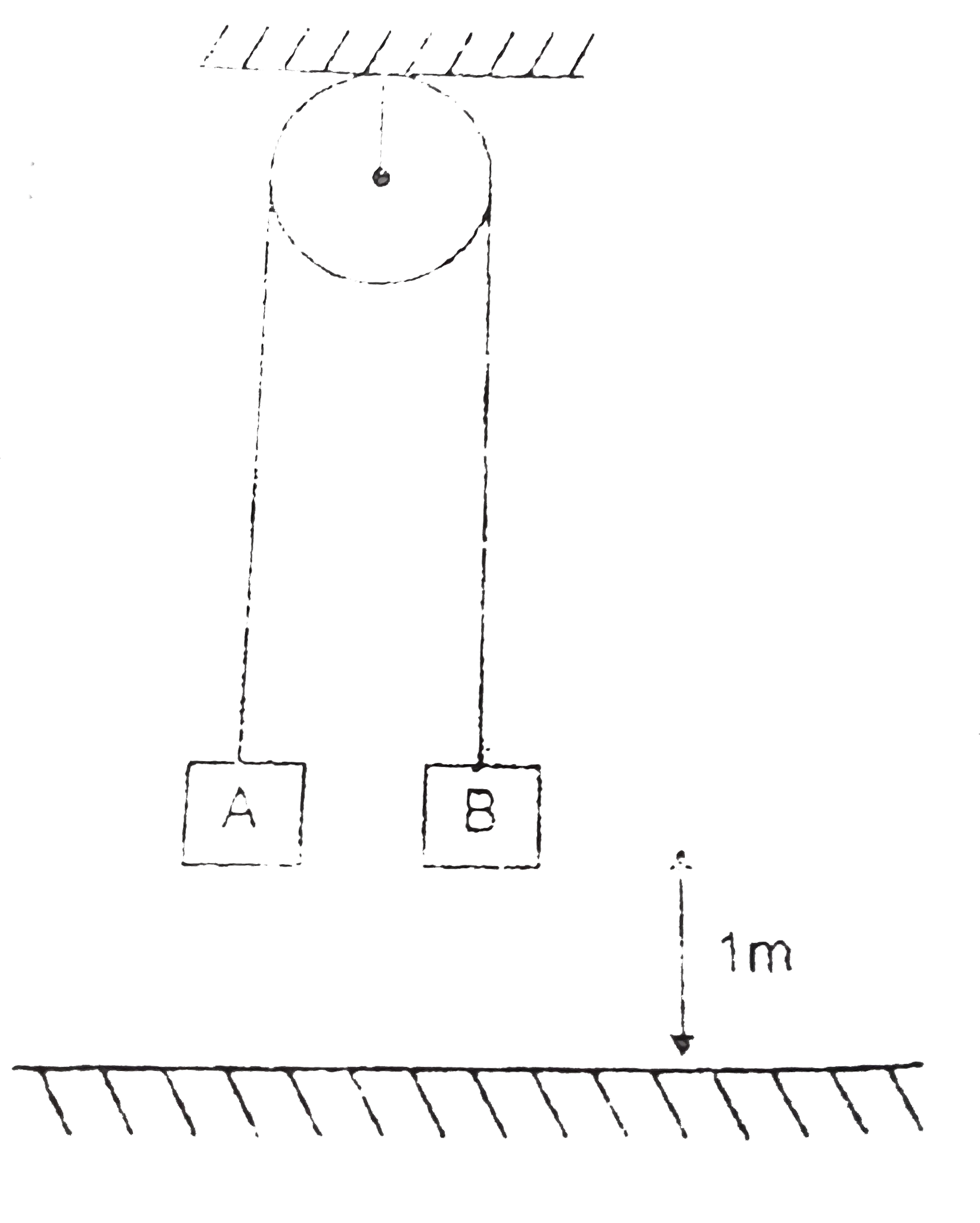
View SolutionTwo masses A and B of 3kg and 2kg are connected by a long inextensible string which passes over a massless and frictionless pulley. Initially the height of both the masses from the ground is same and equal to 1 metre. When the masses are released. Mass A hits the ground and gets stuck to the ground. Consider the length of the string as large, so that the pulley does not obstruct the motion of masses A and B [g=10m/s2]
View SolutionA kite is flying at a height of 30m from the ground. The length of string from the kite to the ground is 60m. Assuming that three is no slack in the string, the angle of elevation of the kite at the ground is: 450 (b) 300 (c) 600 (d) 900
View SolutionA kite is flying at a height of 30m from the ground. The length of string from the kite to the ground is 60m. Assuming that three is no slack in the string, the angle of elevation of the kite at the ground is: 450 (b) 300 (c) 600 (d) 900
View SolutionA kite is flying at a height of 30m from the ground. The length of string from the kite to the ground is 60m. Assuming that there is no slack in the string, the angle of elevation of the kite at the ground is: 450 (b) 300 (c) 600 (d) 900
View SolutionThe angle of depression between a flying kite and 'a' point on the ground is 60 m. If the string makes 30∘.Find the height of the kite from the ground.
View SolutionThe block shown in figure has a mass M and descends with an acceleration a. The mass of the string below the point A is m. Find the tension of the string at the point A and at the lower end.

View SolutionA kite is attached to a string. Find the length of the string , when the height of the kite is 60 m and the string makes an angle 30∘ with the ground .
View Solution