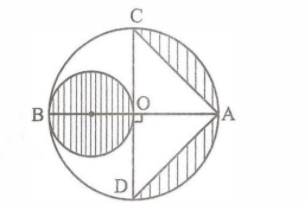
In Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IfOA=7 cm, find the area of the shaded region
We use the concepts of areas of circles and areas of triangles to solve the problem.
AB and CD are diameters of the circle with center O
∴ OD = OC = OA = OB =
Radius of the circle R = 7 cm
∴ AB = 2R = 14 cm
Radius of shaded circular region, r = OD/2 = 7/2 cm
Area of the shaded smaller circular region = πr∘
= π(72cm)2
= 227×72×72cm2= 772cm2= 38.5cm2
Area of the shaded segment of larger circular region = Area of semicircle ACB - Area of ΔABC
= 12π(OA)2−12×AB×OC= 12πR2−12×2R×R
= 12×227×72−12×14×7
= 77−49
= 28cm2
Area of the shaded region = Area of the shaded smaller circular region + Area of the shaded segment of larger circular region
= 38.5cm2+28cm2
= 66.5cm2
Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Exercise 12.2
14 Videos
- AREAS RELATED TO CIRCLESBOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE 12.1
5 Videos
- ARITHMETIC PROGRESSIONSBOOK - NCERT ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - All Questions
65 Videos
Similar Questions
If Figure - 4, AB and CD are two diameter of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IF OA = 7 cm, then find the area of the shaded region.

View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View SolutionIn Figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA=7 cm , find the area of the shaded region.
View SolutionIn Figure -4 AB, and CD are two diameters of a circle with centre O perpendiclualr to each other and OD is the diameter of the circle . If OA = 7 cm , then find the carea of the shaded region .
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn Figure, two circles with centres A and B touch each other at the point C . If AC=8 cm and AB=3 cm , find the area of the shaded region.
View SolutionIn the given figure, the diameter CD of a circle with centre 0 is perpendicular to the chord AB.
If AB = 8 cm and CM = 2 cm, find the radius of the circle.
View SolutionIn figure , AB is a diameter of the circle, AC = 6cm and BC = 8cm . Find the area of the shaded region . (use π=3.14)

View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View Solution
