Show that in a right triangle the hypotenuse is the longest side.
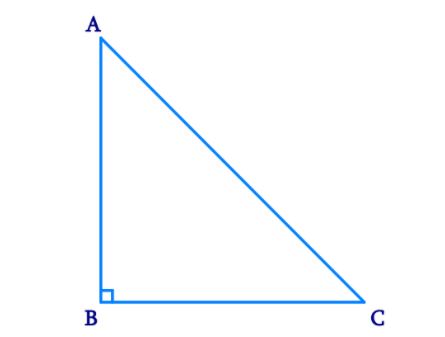
Let us consider a right-angled triangle ABC, right-angled at B.
In ΔABC,
∠A+∠B+∠C=180∘(Angle sum property of a triangle)
∠A+90∘+∠C=180∘
∠A+∠C=90∘
Hence, the other two angles have to be acute (i.e., less than 90∘).
Thus, ∠B is the largest angle in ΔABC.
So, ∠B>∠A and ∠B>∠C
Therefore, AC>BC and AC>AB [Using theorem of triangles, in any triangle, the side opposite to the larger (greater) angle is longer.]
Therefore, AC is the largest side in ΔABC.
However, AC is the hypotenuse of ΔABC.
Therefore, the hypotenuse is the longest side in a right-angled triangle.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.1
8 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Solved Examples
9 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.2
8 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.9
3 Videos
Similar Questions
Knowledge Check
Find the area of a right triangle with hypotenuse of 10 and side of 8
A5B24C40D48
Theorem 6.7 : If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
View SolutionEquilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
View SolutionEquilateral triangles are drawn on the sides of a right triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
View Solution(Pythagoras's Theorem) Prove by vector method that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
View Solution(Pythagoras's Theorem) Prove by vector method that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
View SolutionIf a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.
View SolutionIf a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side of the perpendicular are similar to each other and to the original triangle. Also, prove that the square of the perpendicular is equal to the product of the lengths of the two parts of the hypotenuse.
View Solution
