AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.


Consider two triangles △BOC and △AOD,
In △BOC and△AOD,
∠BOC=∠AOD (Vertically opposite angles)
∠CBO=∠DAO (Each 90∘, since AD and BC are perpendicular to AB)
BC=AD (Given)
∴△BOC≅△AOD (AAS congruence rule)
∴ BO=AO (By CPCT)
Thus, CD bisects AB and O is the mid-point of AB.
Topper's Solved these Questions
- TRIANGLESBook:NCERT ENGLISHChapter:TRIANGLESExercise:Solved Examples
Explore 9 Videos
- TRIANGLESBook:NCERT ENGLISHChapter:TRIANGLESExercise:EXERCISE 7.5
Explore 4 Videos
- TRIANGLESBook:NCERT ENGLISHChapter:TRIANGLESExercise:EXERCISE 7.4
Explore 6 Videos
- SURFACE AREAS AND VOLUMESBook:NCERT ENGLISHChapter:SURFACE AREAS AND VOLUMESExercise:Exercise 13.9
Explore 3 Videos
Similar Questions
AD and BC are equal perpendiculars to a line segment AB . Show that CD bisects AB.
View SolutionAD and BC are equal perpendiculars to a line segment AB . Show that CD bisects AB.
View SolutionAD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
View SolutionIn ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.
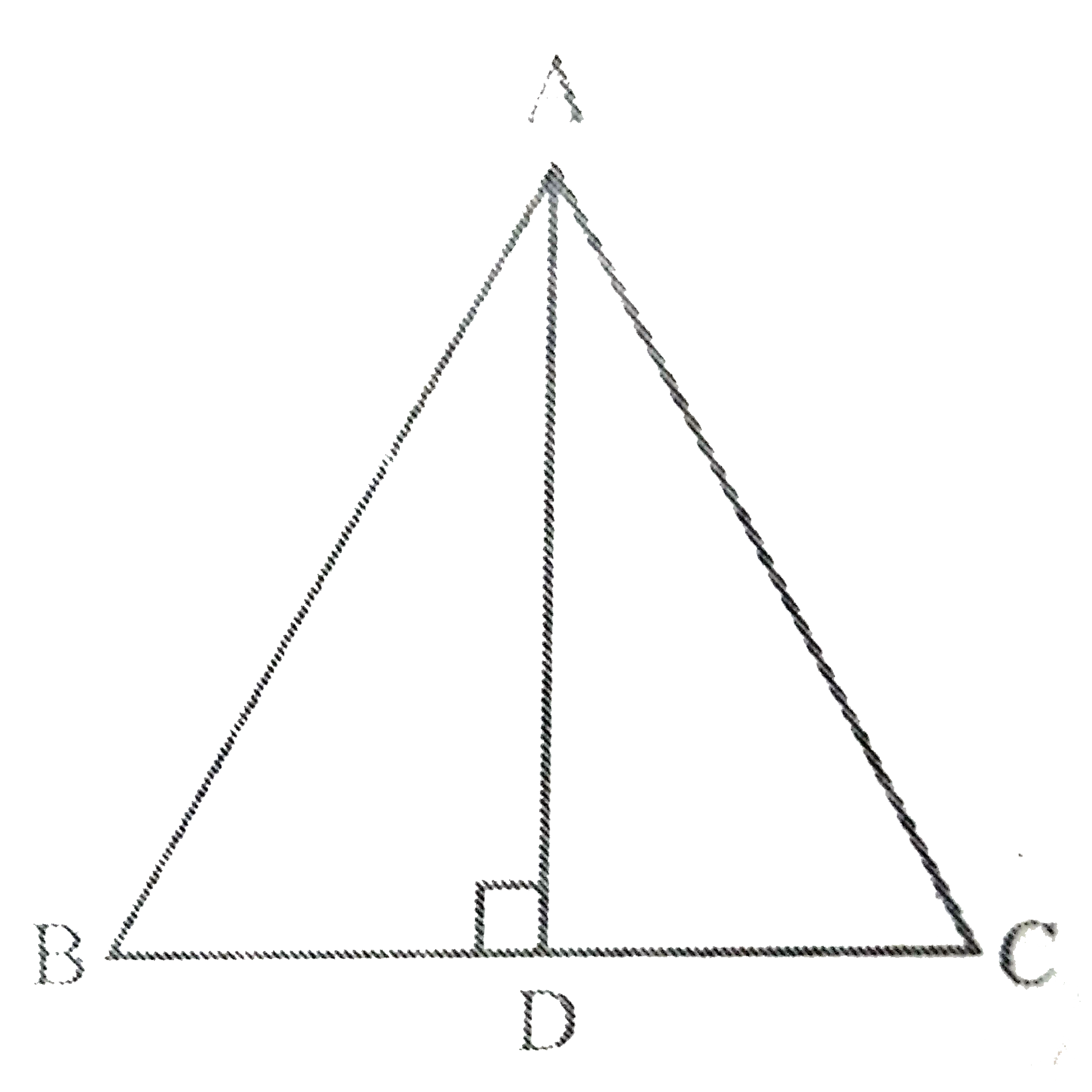
View SolutionIn Δ ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that AB = ACand ΔABCis isosceles
View SolutionDraw a line segment EF equal to a given line segment AB
View SolutionDraw a perpendicular to a given line segment AB though a point P lying outside AB.
View SolutionThe following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively. Show that :
CD×AB=CA×DE
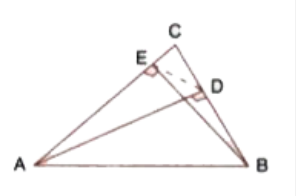
View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.

View SolutionIn the given figure, AC is perpendicular to line PQ and BC = CD. Show that AE is greater than AB.
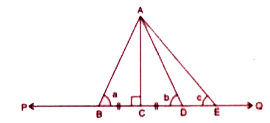
View Solution
