Deduce the equations of unifromly accelerated motion in one dimension by following calculus method.
By definition
a=dvdt
dv=adt
Integrating both sides
∫vv0dv=∫t0adt
=a∫t0dt (a is constant)
v−v0=at
v=v0+at
Further, v=dxdt ltbr> dx=vdt
Integrating both sides
∫xx0dx=∫t0vdt
=∫t0(v0+at)dt
x−x0=v0t+12at2
x=x0+v0t+12at2
We can write
a=dvdt=dvdxdxdt=vdvdx
or, vdv=adx
Integrating both sides
∫vv0vdv=∫xx0adx
v2−v202=a(x−x0)
v2=v20+2a(x−x0)
The advantage of this method is that it can be used for motion with non-uniform acceleration also.
Now, we shall use these equations to some important cases.
Topper's Solved these Questions
Similar Questions
Write three equations of uniformly accelerated motion relating the initial velocity (u), final velocity (v), time (t), acceleration (a) and displacement (S).
View SolutionDraw velocity – time graph of uniformly accelerated motion in one dimension. From the velocity – time graph of uniform accelerated motion, deduce the equations of motion in distance and time.
View Solution
Knowledge Check
Checking the correctness of equations using the method of dimensions is based on
Athe type of systemBequality of inertial frames of referencesCprinciple of homogeneity of dimensionsDnone of these
What is nature of trajectory of a particle having a uniformly accelerated motion in a plane?
View SolutionWhich of the following curves does not represent motion in one dimensions?
View SolutionDerive following equations for a uniformly accelerated motion :
(i) v = u + at
(ii) S=ut+12at2
(iii) v2=u2+2aS
Where the symbols have their usual meanings .
View SolutionThe relation between position (x) and time (t) are given below for a particle moving along a straight line. Which of the following equation represents uniformly accelerated motion? [where αandβ are positive constants]
View SolutionDerive the equations of rotational motion for a body moving with uniform angular acceleration,
View SolutionCan a body moving in two dimensional plane has a acceleration in only one dimension? Given an example.
View SolutionA particle is projected from level ground near the surface of earth with intitial velocity →u=uxˆi+uyˆj ,as shown in the figure. If a(x)anday are the components of acceleration in horizontal and vertically downward directions then
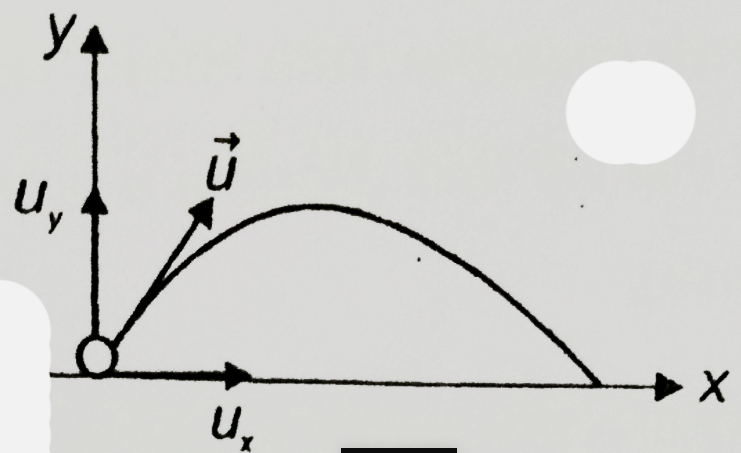
Match the following columns.
(Column I,Column II), ( (A) Projectile motion,(p) Uniform motion)((B) A block sent sliding on a smooth horizontal surface,(q) Unifromly accelerated motion),((C) Unifrom circular motion , (r) motion with non- uniform acceleration),( (D) Swing of pendulum ,(s) Non-uniform motion):}
View Solution
