The wires which connect the battery of an automobile to its starting motor carry a current of 300A (for a short time). What is the force per unit length between the wires if they are 70cm long and 1⋅5cm apart? Is the force attractive or repulsive?
To solve the problem, we need to calculate the force per unit length between two parallel wires carrying the same current. We will use the formula for the magnetic force per unit length between two parallel current-carrying wires.
1. Identify the Given Values:
- Current (I) = 300 A
- Length of the wires (L) = 70 cm = 0.7 m (conversion from cm to m)
- Distance between the wires (r) = 1.5 cm = 0.015 m (conversion from cm to m)
2. Use the Formula for Force per Unit Length:
The formula for the force per unit length (F/L) between two parallel wires carrying current is given by:
FL=μ0I22πr
where:
- μ0 (permeability of free space) = 4π×10−7T m/A
3. Substitute the Values into the Formula:
FL=(4π×10−7)×(300)22π×0.015
4. Simplify the Expression:
- First, calculate 3002:
3002=90000
- Now substitute this value:
FL=(4π×10−7)×900002π×0.015
- The π cancels out:
FL=4×10−7×900002×0.015
5. Calculate the Numerator and Denominator:
- Calculate the numerator:
4×10−7×90000=3.6×10−2
- Calculate the denominator:
2×0.015=0.03
6. Calculate the Force per Unit Length:
FL=3.6×10−20.03=1.2N/m
7. Determine the Nature of the Force:
Since the currents in both wires are in the same direction, the force between the wires is attractive.
Final Answer:
The force per unit length between the wires is 1.2N/m and the force is attractive.
- Current (I) = 300 A
- Length of the wires (L) = 70 cm = 0.7 m (conversion from cm to m)
- Distance between the wires (r) = 1.5 cm = 0.015 m (conversion from cm to m)
The formula for the force per unit length (F/L) between two parallel wires carrying current is given by:
FL=μ0I22πr
where:
- μ0 (permeability of free space) = 4π×10−7T m/A
FL=(4π×10−7)×(300)22π×0.015
- First, calculate 3002:
3002=90000
- Now substitute this value:
FL=(4π×10−7)×900002π×0.015
- The π cancels out:
FL=4×10−7×900002×0.015
- Calculate the numerator:
4×10−7×90000=3.6×10−2
- Calculate the denominator:
2×0.015=0.03
FL=3.6×10−20.03=1.2N/m
Since the currents in both wires are in the same direction, the force between the wires is attractive.
The force per unit length between the wires is 1.2N/m and the force is attractive.
Topper's Solved these Questions
Similar Questions
Two long parallel wires are at a distance of 1 m. Both of them carry 1A of current. The force of attraction per unit length between the two wires is
View SolutionTwo thin long parallel wires seperated by a distance 'b' are carrying a current ' I' amp each . The magnitude of the force3 per unit length exerted by one wire on the other is
View Solution
Knowledge Check
Two parallel wires 2 m apart carry currents of 2 A and 5 A respectively in same direction, the force per unit length acting between these two wires is
A2×10−6Nm−1B3×10−6Nm−1C1×10−6Nm−1D4×10−6Nm−1
Derive the expression for force per unit length between two long straight parallel current carrying conductors. Hence define one ampere.
View SolutionTwo long, parallel wires are separated by a distance of 0.400m (as shown in Fig.) The current I1andI2 have the direction shown.
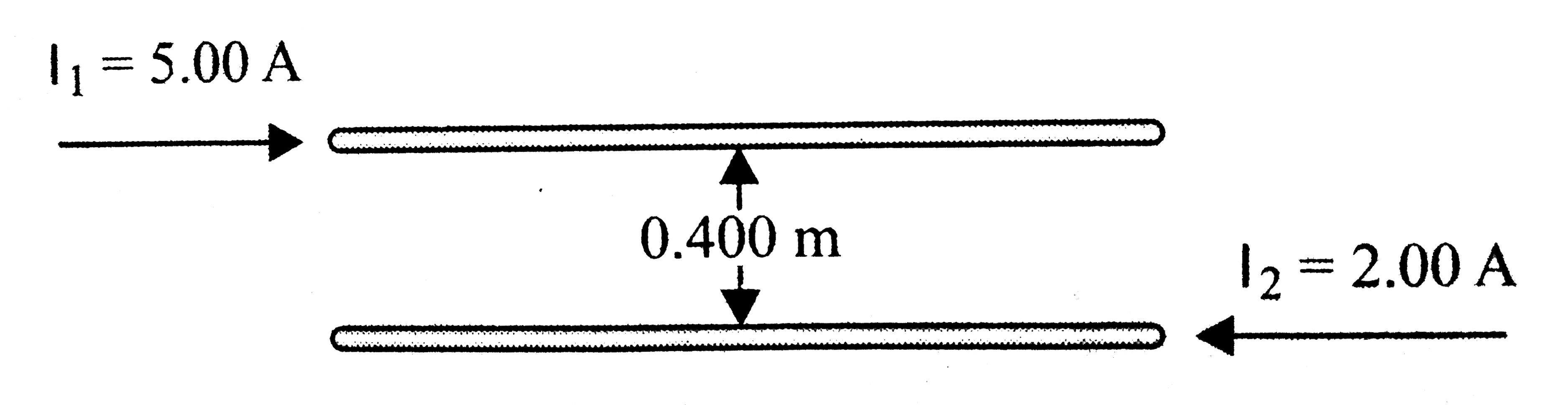
(a) Calculate the magnitude of the force exerted by each wire on a 1.20m length of the other. Is the force attractive or repulsive ?
(b) Each current is doubled, so that I1 becomes 10.0A and I2 becomes 4.00A. Now, what is the magnitude of the force that each wire exerts on a 1.20m length of the other?
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View SolutionWhen two parallel wires carrying current l and 2l in same direction are placed at a distance d apart, the ratio of force per unit length acting upon the wire due to other is
View SolutionA semi circular arc of radius r and a straight wire along the diameter, both are carrying same current i find out magnetic force per unit length on the small element P, which is at the centre of curvature.

View SolutionCalculate the force per unit length on a long straight wire carrying current 4A due to parallel wire carrying current 6A current. Distance between the wires =3cm.
View SolutionTwo long parallel wires are 30 cm apart carrying currents 10 A and 15 A respectively in the same direction. The force acting over a length of 5 m of the wires is
View Solution
