In a certain region of space, electric field is along the z-direction throughout. The magnitude of electric field is , however, not constant but increases uniformly along the positive z-direction. At the rate of 105NC−1m−1 . What are the force and torque experienced by system having a total dipole moment equal to 10−7Cm in the negative z-direction?
To solve the problem, we need to calculate the force and torque experienced by a dipole in a non-uniform electric field. Let's go through the steps systematically.
Step 1: Understand the Electric Field Variation
The electric field E is directed along the positive z-direction and increases uniformly at a rate of 105N/C/m. This means that the electric field at a distance z from the origin can be expressed as:
E(z)=E0+(105N/C/m)⋅z
where E0 is the electric field at z=0.
Step 2: Calculate the Force on the Dipole
The dipole moment →p is given as 10−7C m in the negative z-direction, i.e., →p=−10−7^k.
The force →F on a dipole in a non-uniform electric field is given by:
→F=Q→E+(−Q)→E′=Q→E−Q→E′
where →E′ is the electric field at the position of the negative charge of the dipole.
For a dipole, the net force can be expressed as:
→F=−→pdEdz
Here, dEdz=105N/C/m and →p=−10−7^k.
Substituting these values:
→F=−(−10−7^k)⋅(105)=10−7⋅105^k=10−2^k
Thus, the force experienced by the dipole is:
→F=10−2^kN
Step 3: Calculate the Torque on the Dipole
The torque →τ on a dipole in an electric field is given by:
→τ=→p×→E
Since →p is in the negative z-direction and →E is in the positive z-direction, the angle θ between →p and →E is 180∘.
Using the sine of the angle:
sin(180∘)=0
Thus, the torque becomes:
→τ=→p×→E=0
Final Results
1. The force experienced by the dipole is:
→F=10−2^kN
2. The torque experienced by the dipole is:
→τ=0
The electric field E is directed along the positive z-direction and increases uniformly at a rate of 105N/C/m. This means that the electric field at a distance z from the origin can be expressed as:
E(z)=E0+(105N/C/m)⋅z
where E0 is the electric field at z=0.
The dipole moment →p is given as 10−7C m in the negative z-direction, i.e., →p=−10−7^k.
→F=Q→E+(−Q)→E′=Q→E−Q→E′
where →E′ is the electric field at the position of the negative charge of the dipole.
→F=−→pdEdz
Here, dEdz=105N/C/m and →p=−10−7^k.
→F=−(−10−7^k)⋅(105)=10−7⋅105^k=10−2^k
Thus, the force experienced by the dipole is:
→F=10−2^kN
The torque →τ on a dipole in an electric field is given by:
→τ=→p×→E
Since →p is in the negative z-direction and →E is in the positive z-direction, the angle θ between →p and →E is 180∘.
sin(180∘)=0
Thus, the torque becomes:
→τ=→p×→E=0
1. The force experienced by the dipole is:
→F=10−2^kN
2. The torque experienced by the dipole is:
→τ=0
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise
34 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - All Questions
32 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
17 Videos
Similar Questions
In a certain region of space, the electric field is along +y-direction and has a magnitude of 400 V/m . What is the potential difference from the coordinate origin to the following points?
a.x=0,y=20cm,z=0
b. x=0,y=−30cm,z=0
c.x=0,y=0,z=15cm
View SolutionIn a certain region of space, the potential is given by V=k(2x2−y2+z2). The electric field at the point (1, 1, 1) has magnitude:
View Solution
Knowledge Check
A uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
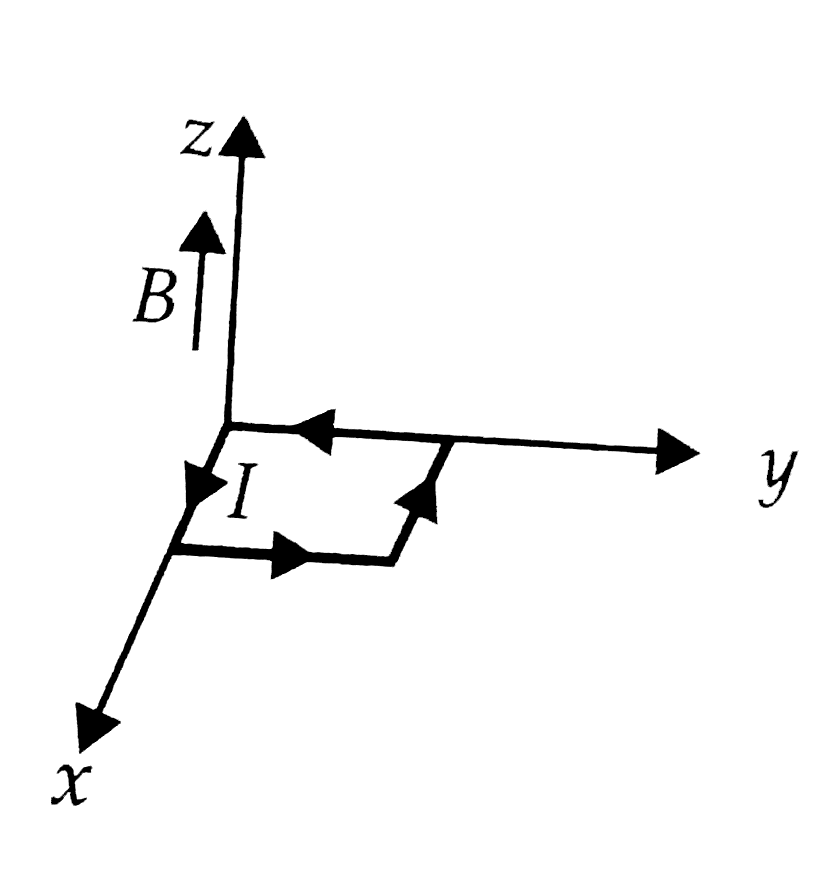 AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
A square loop of side 12 cm with its sides parallel to X and Y axes is moved with a velocity of 8 cm s−1 in the positive x-direction in an environment containing a magnetic field in the positive z-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10−3Tcm−1 along the negative x-direction (that is it increases by 10−3Tcm−1as one moves in the negative x-direction), and it is decreasing in time at the rate of 10−3Ts−1. Determine the direction and magnitude of the induced current in the loop if its resistance is 4.50 mΩ.
View SolutionA plane electromagnetic wave travels in vacuum along z-direction. What can you say about the direction of electric and magnetic field vectors?
View SolutionA proton is moving with a velocity of 5×105m/s along the Y-direction. It is acted upon by an electric field of intensity 105 V/m along the X-direction and a magnetic field of 1Wb/m2 along the Z-direction. Then the Lorentz force on the particle is :
View SolutionThe electric potential in a region is given by the relation V(x)=4+5x2. If a dipole is placed at position (-1,0) with dipole moment →P pointing along positive y-direction, then
View SolutionThere exists an electric field of 1NC−1 along Y direction. The flux passing through the square of 1 m placed in xy−plane inside the electric field is
View SolutionA plane electromagnetic wave of frequency 28 MHz travels in free space along the positive x-direction . At a particular point in space and time, electric field is 9.3 V/m along positive y-direction. The magnetic field (in T) at that point is
View SolutionIn a region of space, magnetic field exists in a cylindrical region of radius a centred at origin with magnetic field along negative z-direction. The field is given by →B=−B0tˆk. The force experienced by a stationary charge q placed at (r, 0, 0), where r>a is
View Solution