Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss's law. [Hint.use Coulomb's law directly and evaluate the necessary integral ].
To derive the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss's law, we will directly apply Coulomb's law and evaluate the necessary integral. Here’s a step-by-step solution:
Step 1: Define the Problem
Consider a long thin wire of length L with a uniform linear charge density λ (charge per unit length). We want to find the electric field E at a point P located at a perpendicular distance R from the wire.
Step 2: Consider a Small Element of Charge
Take a small element of the wire dx at a distance x from the point P. The charge dq on this small element is given by:
dq=λdx
Step 3: Apply Coulomb's Law
According to Coulomb's law, the electric field dE due to the charge dq at point P is given by:
dE=14πϵ0dqr2
where r is the distance from the charge element dq to the point P. Using the Pythagorean theorem, we find:
r=√R2+x2
Thus, we can write:
dE=14πϵ0λdxR2+x2
Step 4: Resolve the Electric Field into Components
The electric field dE has two components: one along the direction of the wire (horizontal) and one perpendicular to the wire (vertical). The horizontal components from symmetrically located charge elements will cancel out, leaving only the vertical component.
Let θ be the angle between the line connecting dq to point P and the perpendicular line from the wire to point P. The vertical component of dE is:
dEy=dEcosθ
Using the definition of cosine:
cosθ=R√R2+x2
Thus,
dEy=dEcosθ=14πϵ0λdxR2+x2⋅R√R2+x2=λRdx4πϵ0(R2+x2)3/2
Step 5: Integrate to Find the Total Electric Field
To find the total electric field E at point P, we integrate dEy from −∞ to +∞:
E=∫∞−∞dEy=∫∞−∞λRdx4πϵ0(R2+x2)3/2
Step 6: Evaluate the Integral
The integral can be evaluated using a standard integral result:
∫∞−∞dx(R2+x2)3/2=2R2
Thus, we have:
E=λR4πϵ0⋅2R2=λ2πϵ0R
Final Result
The electric field E due to a long thin wire of uniform linear charge density λ at a distance R from the wire is given by:
E=λ2πϵ0R
Consider a long thin wire of length L with a uniform linear charge density λ (charge per unit length). We want to find the electric field E at a point P located at a perpendicular distance R from the wire.
Take a small element of the wire dx at a distance x from the point P. The charge dq on this small element is given by:
dq=λdx
According to Coulomb's law, the electric field dE due to the charge dq at point P is given by:
dE=14πϵ0dqr2
where r is the distance from the charge element dq to the point P. Using the Pythagorean theorem, we find:
r=√R2+x2
Thus, we can write:
dE=14πϵ0λdxR2+x2
The electric field dE has two components: one along the direction of the wire (horizontal) and one perpendicular to the wire (vertical). The horizontal components from symmetrically located charge elements will cancel out, leaving only the vertical component.
dEy=dEcosθ
Using the definition of cosine:
cosθ=R√R2+x2
Thus,
dEy=dEcosθ=14πϵ0λdxR2+x2⋅R√R2+x2=λRdx4πϵ0(R2+x2)3/2
To find the total electric field E at point P, we integrate dEy from −∞ to +∞:
E=∫∞−∞dEy=∫∞−∞λRdx4πϵ0(R2+x2)3/2
The integral can be evaluated using a standard integral result:
∫∞−∞dx(R2+x2)3/2=2R2
Thus, we have:
E=λR4πϵ0⋅2R2=λ2πϵ0R
The electric field E due to a long thin wire of uniform linear charge density λ at a distance R from the wire is given by:
E=λ2πϵ0R
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:NCERT ENGLISHChapter:ELECTRIC CHARGES AND FIELDSExercise:Exercise
Explore 34 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:NCERT ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTERExercise:All Questions
Explore 32 Videos
- ELECTROMAGNETIC INDUCTIONBook:NCERT ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercise
Explore 17 Videos
Similar Questions
Find the electric field at point O, due to the segment of a ring, whose linear charge density is 8C/cm

View SolutionAnswer the following:
(a) State Gauss' law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ.
(b) A wire AB of length L has linear charge density λ=kx, where x is measured from the end A of the wire.
This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.
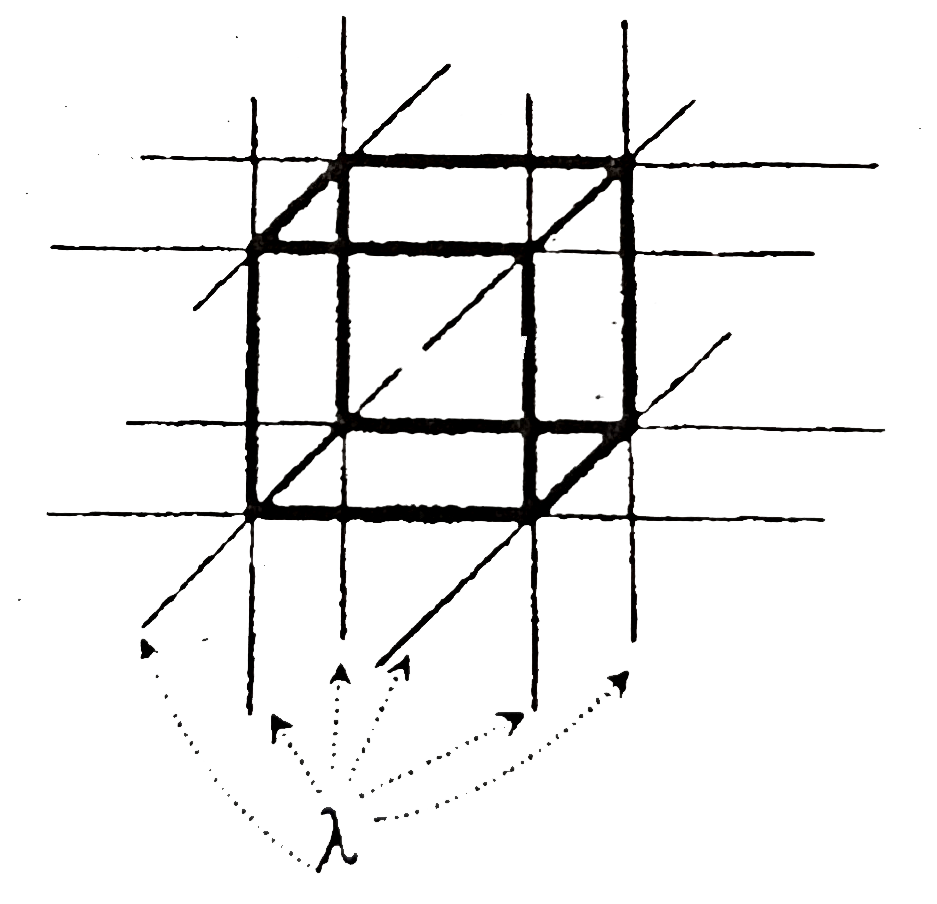
View SolutionTwelve infinite long wire of uniform linear charge density (λ) are passing along the twelve edges of a cube. Find electric flux through any face of cube. ,
View SolutionFigure shows a long wire having uniform charge density λ as shown in figure. Calculate electric field intensity at point P.
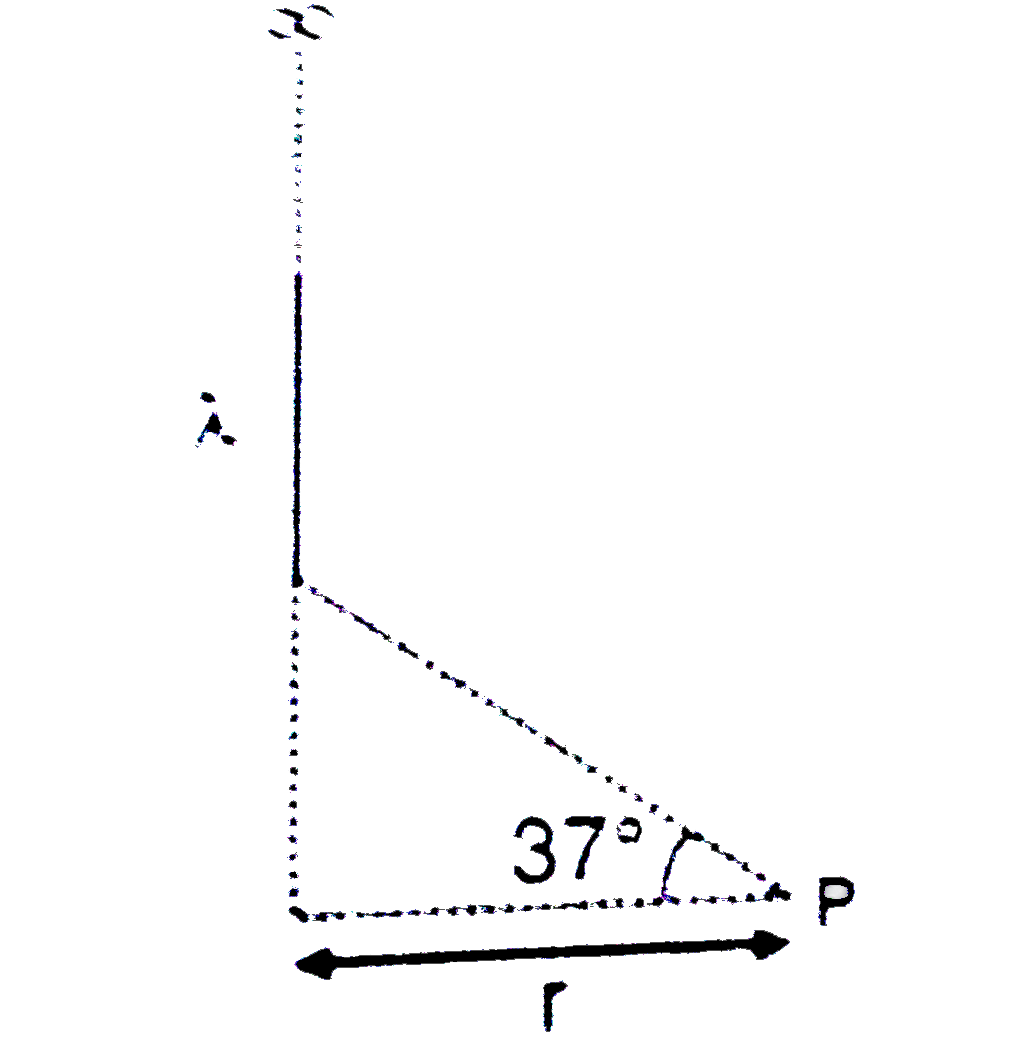
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
View SolutionA long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
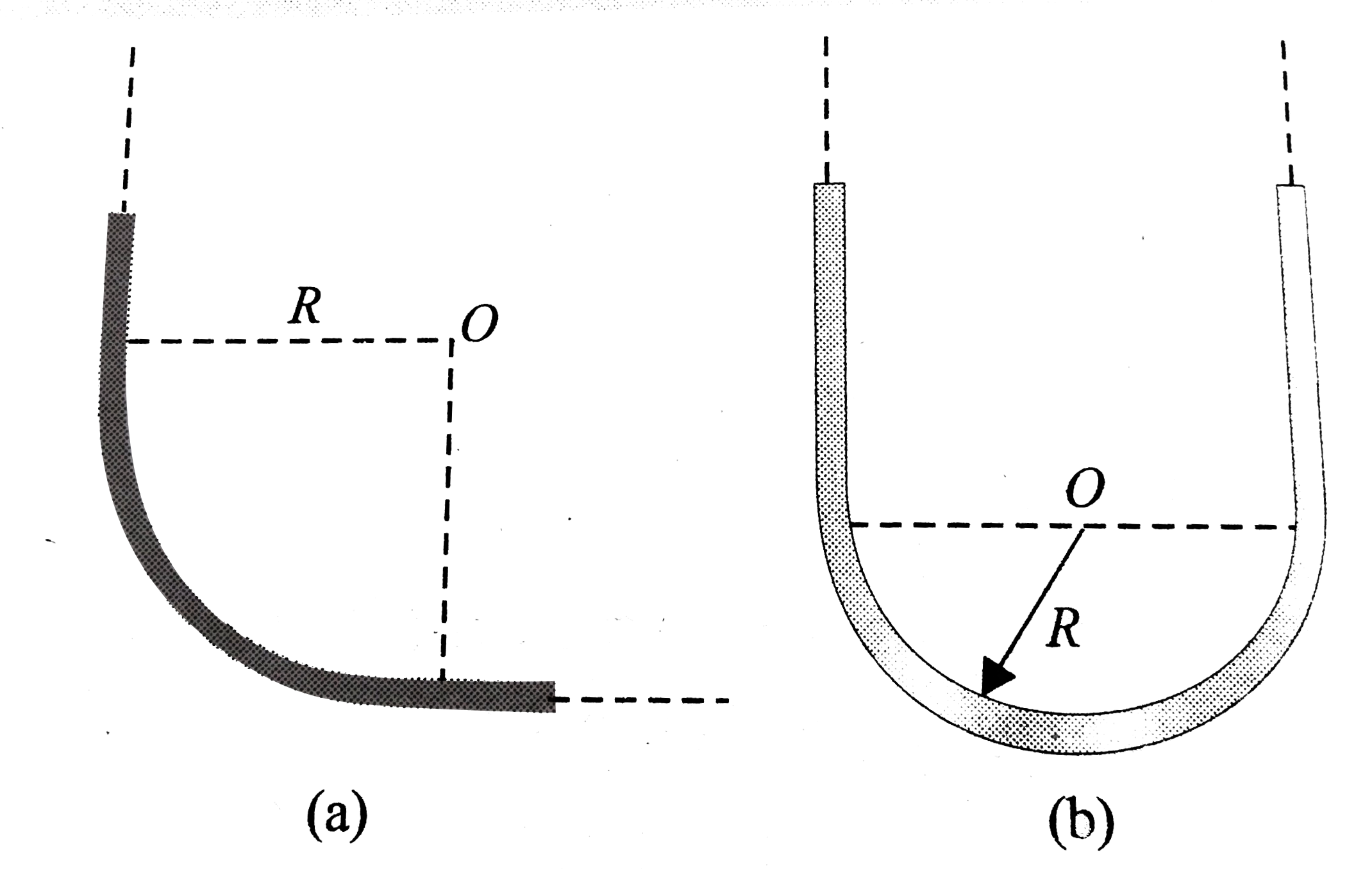
View SolutionFind electric field at point A, B, C, D due to infinitely long uniformly charged wire with linear charge density λ and kept along z-axis (as shown in figure). Assume that all the parameters are in S.l. units.

View SolutionAn infinitely long thin straight wire has uniform linear charge density of 1/3coulm−1 .Then the magnitude of the electric intensity at a point 18cm away is
View SolutionLet E1(r), E2(r) and E3(r) be the respectively electric field at a distance r from a point charge Q, an infinitely long wire with constant linear charge density λ, and an infinite plane with uniform surface charge density σ. If E1(r0)=E2(r0)=E3(r0) at a given distance r0, then
View Solution