An astronaut accidentally gets separated out his small spaceship accelerating in interstellar space at a constant rate of 100ms−2 . What is the acceleration of the astronaut the instant after he is outside the spaceship? (Assume that there are no nearby stars to exert gravitional force on him)
To solve the problem, we need to analyze the situation of the astronaut after he gets separated from the spaceship. Here’s the step-by-step solution:
Step 1: Understand the scenario
The astronaut is initially inside a spaceship that is accelerating at a constant rate of 100m/s2. When he gets separated from the spaceship, we need to determine his acceleration at that instant.
Step 2: Identify forces acting on the astronaut
Since the problem states that there are no nearby stars to exert gravitational force on the astronaut, we need to consider the forces acting on him. The only forces that could act on him would be gravitational forces from nearby celestial bodies or the spaceship itself.
Step 3: Analyze gravitational forces
1. Gravitational force from stars: Given that there are no nearby stars, this force is zero.
2. Gravitational force from the spaceship: The spaceship is described as a small spaceship, which implies that it does not have significant mass to exert a gravitational force on the astronaut. Therefore, this force is also effectively zero.
Step 4: Calculate the net force on the astronaut
Since both gravitational forces are zero, the net gravitational force acting on the astronaut is:
Fnet=Fgravity from stars+Fgravity from spaceship=0+0=0
Step 5: Apply Newton's second law
According to Newton's second law, the net force acting on an object is equal to the mass of the object multiplied by its acceleration:
Fnet=m⋅a
Since we have established that Fnet=0, we can write:
0=m⋅a
Step 6: Solve for acceleration
Since the mass m of the astronaut cannot be zero, the only way for the equation to hold true is if the acceleration a is zero:
a=0
Conclusion
The acceleration of the astronaut the instant after he is outside the spaceship is 0m/s2.
---
The astronaut is initially inside a spaceship that is accelerating at a constant rate of 100m/s2. When he gets separated from the spaceship, we need to determine his acceleration at that instant.
Since the problem states that there are no nearby stars to exert gravitational force on the astronaut, we need to consider the forces acting on him. The only forces that could act on him would be gravitational forces from nearby celestial bodies or the spaceship itself.
1. Gravitational force from stars: Given that there are no nearby stars, this force is zero.
2. Gravitational force from the spaceship: The spaceship is described as a small spaceship, which implies that it does not have significant mass to exert a gravitational force on the astronaut. Therefore, this force is also effectively zero.
Since both gravitational forces are zero, the net gravitational force acting on the astronaut is:
Fnet=Fgravity from stars+Fgravity from spaceship=0+0=0
According to Newton's second law, the net force acting on an object is equal to the mass of the object multiplied by its acceleration:
Fnet=m⋅a
Since we have established that Fnet=0, we can write:
0=m⋅a
Since the mass m of the astronaut cannot be zero, the only way for the equation to hold true is if the acceleration a is zero:
a=0
The acceleration of the astronaut the instant after he is outside the spaceship is 0m/s2.
Topper's Solved these Questions
Similar Questions
An astronaut accidentally gets separateed out of his small spaceship accelerating in inter-stellar space at a constant rate of 50ms−2. What is the acceleration of the astronaut the instant after he is outside the spaceship? (Assume that there are no nearby stars to exert gravitational force on him.)
View SolutionAn astronaut accidentally gets thrown out of his small spaceship accelerating in interstellar space at a constant rate. What is the acceleration of the astronaut, the instant after he is outside the spaceship?
View Solution
Knowledge Check
A cyclist is riding with a speed of 27kmh−1. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate 0.5ms−2. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn ?
A0.68 m s−2B0.86 m s−2C0.56 m s−2D0.76 m s−2
Suppose the acceleration due to gravity at earth's surface is 10ms−2 and at the surface of Mars it is 4.0ms−2. A passenger goes from the earth to the mars in a spaceship with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time?
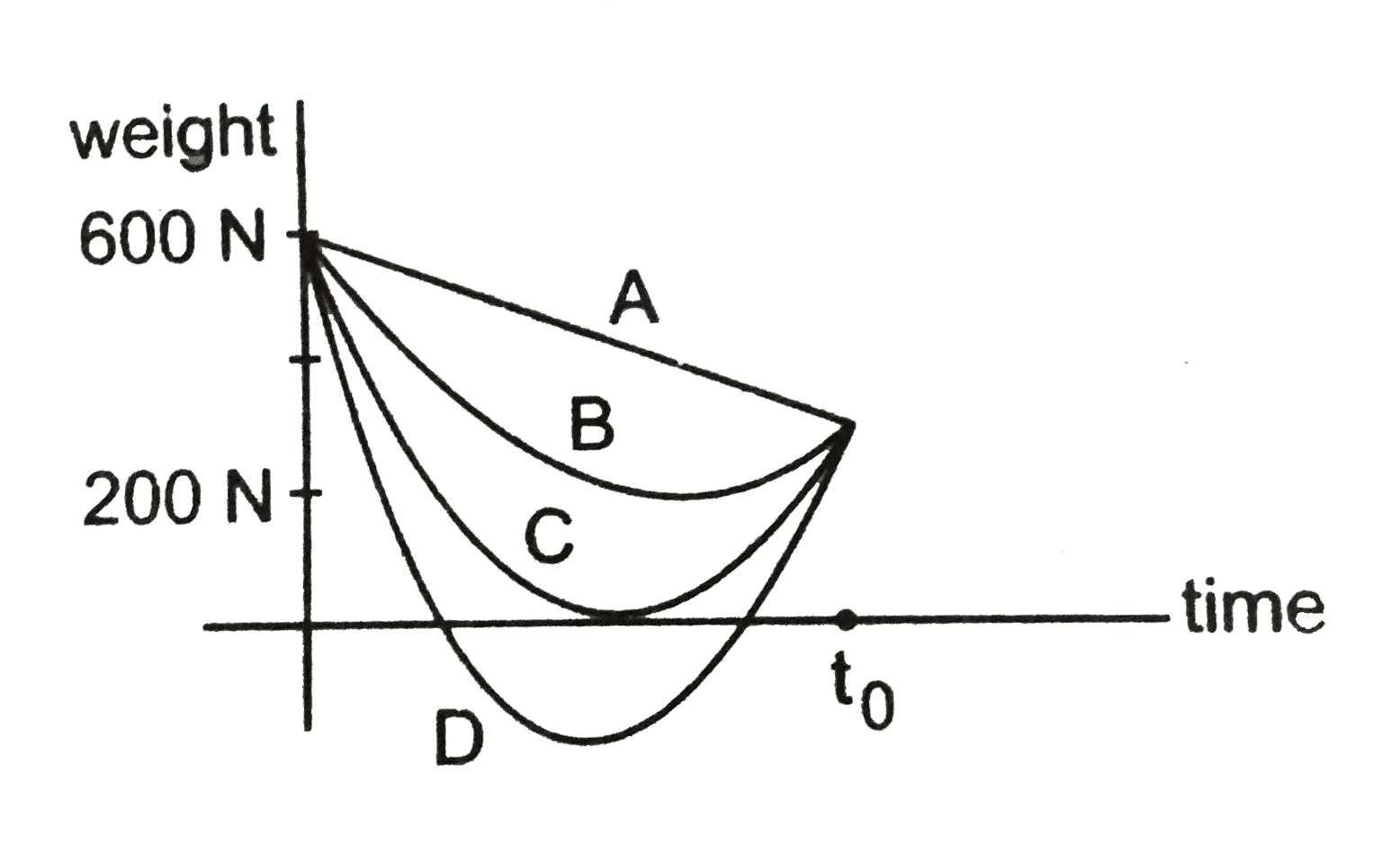
View SolutionA cylclist is riding with a speed of 27kmh−1. As he approaches a circular turn on the road of radius 80m, he applies brakes and reduces his speed at the constant rate of 0.5ms−2. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn ?
View SolutionIf accleration due to gravity on the surface of earth is 10ms−2 and let acceleration due to gravitational acceleration at surface of another planet of our solar system be 5ms−2 An astronaut weighing 50kg on earth goes to this planet in spaceship with a constant velcity The weight of the astronaut with time of fiight is roughly given by
.
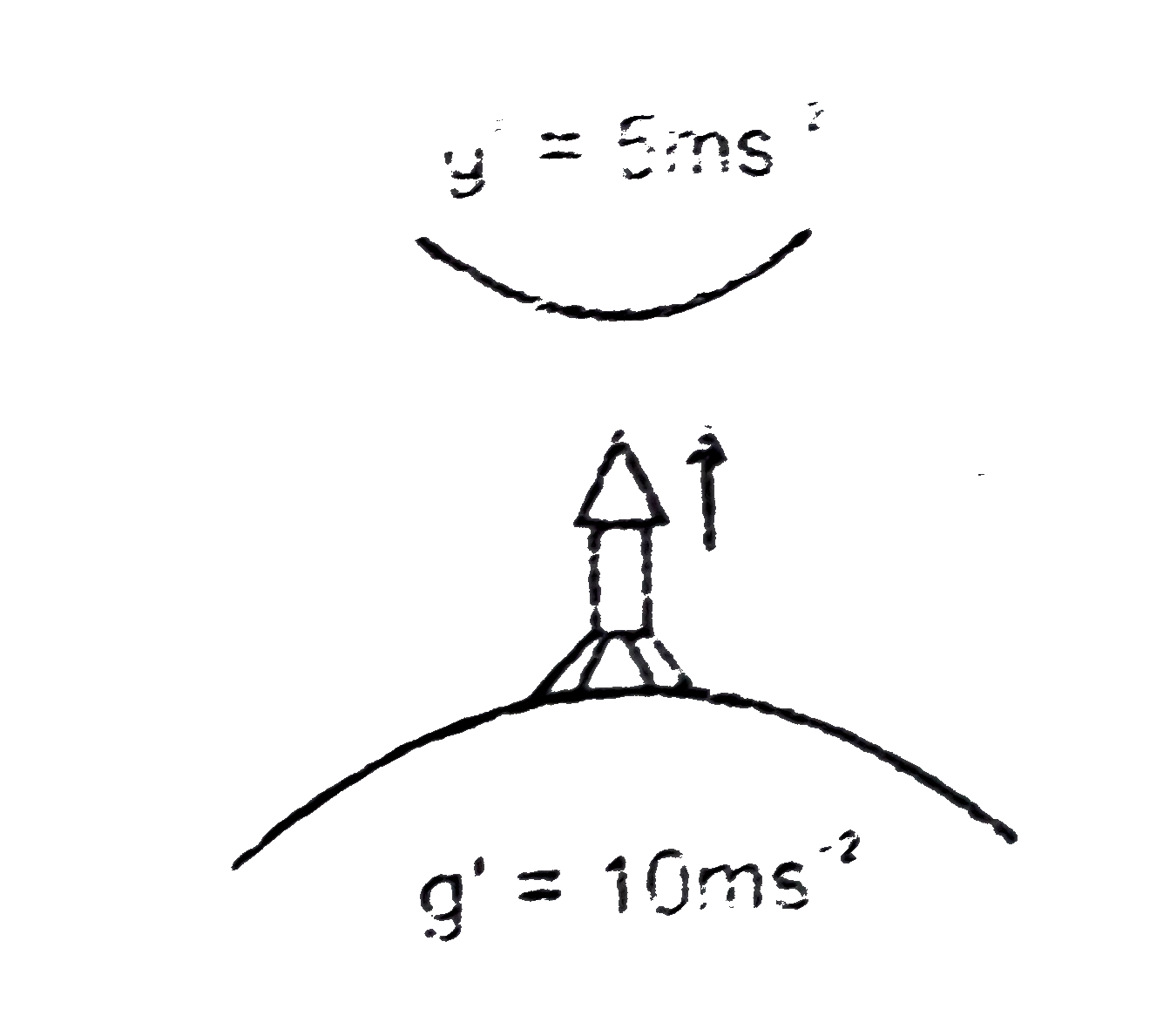View SolutionTwo vertical cylinders are connected by a small tube at the bottom. It contains a gas at constant temperature . Initially the pistons are located at the same height. The diameters of the two cylinders are different . Outside the cylinder the space is vaccum . Gravitational acceleration is h,h0=20cm,m1=2kgandm2=1kg. The pistons are initially in equilibrium. If the masses of the piston are interchanged find the separation between the two pistons when they are again in equilibrium. Assume constant temperature .
_E01_299_Q01.png)
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
The ratio of the energy consumed by the camel during uniform motion for the two cases when it moves with speed 5ms−1 to the case when it moves with 10ms−1
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Sign of work done by the camel on the load during parts of motion, accelerated motion, uniform motion and retarded motion, respectively are
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Maximum power transmitted by the camel to load is
View Solution