Two bodies of masses 10 kg and 20 kg respectively kept on a smooth horizontal surface are tied to the ends of a light string A horizontal force F = 600 N is applied to (i) A and (ii) B along the direction of string. What is the tension in the string in each case ?
To solve the problem, we need to analyze the two scenarios separately: when the force is applied to mass A and when it is applied to mass B.
Step 1: Analyze the first case (Force applied to A)
1. Identify the masses and force:
- Mass of A (m_A) = 10 kg
- Mass of B (m_B) = 20 kg
- Applied force (F) = 600 N
2. Draw a free body diagram for mass A:
- The forces acting on A are:
- Applied force (F) = 600 N (to the right)
- Tension in the string (T) (to the left)
3. Write the equation of motion for mass A:
F−T=mA⋅a(1)
Substituting the values:
600−T=10a(1)
4. Draw a free body diagram for mass B:
- The only force acting on B is the tension (T) in the string.
5. Write the equation of motion for mass B:
T=mB⋅a(2)
Substituting the values:
T=20a(2)
6. Combine the equations:
From equation (1):
600−T=10a
Substitute equation (2) into this:
600−20a=10a
Rearranging gives:
600=30a
Thus:
a=60030=20m/s2
7. Find the tension (T):
Substitute the value of acceleration back into equation (2):
T=20a=20×20=400N
Step 2: Analyze the second case (Force applied to B)
1. Draw a free body diagram for mass B:
- The forces acting on B are:
- Applied force (F) = 600 N (to the right)
- Tension in the string (T) (to the left)
2. Write the equation of motion for mass B:
600−T=mB⋅a(3)
Substituting the values:
600−T=20a(3)
3. Draw a free body diagram for mass A:
- The only force acting on A is the tension (T) in the string.
4. Write the equation of motion for mass A:
T=mA⋅a(4)
Substituting the values:
T=10a(4)
5. Combine the equations:
From equation (3):
600−T=20a
Substitute equation (4) into this:
600−10a=20a
Rearranging gives:
600=30a
Thus:
a=60030=20m/s2
6. Find the tension (T):
Substitute the value of acceleration back into equation (4):
T=10a=10×20=200N
Final Results:
- Tension when the force is applied to A: 400 N
- Tension when the force is applied to B: 200 N
- Mass of A (m_A) = 10 kg
- Mass of B (m_B) = 20 kg
- Applied force (F) = 600 N
- The forces acting on A are:
- Applied force (F) = 600 N (to the right)
- Tension in the string (T) (to the left)
F−T=mA⋅a(1)
Substituting the values:
600−T=10a(1)
- The only force acting on B is the tension (T) in the string.
5. Write the equation of motion for mass B:
T=mB⋅a(2)
Substituting the values:
T=20a(2)
From equation (1):
600−T=10a
Substitute equation (2) into this:
600−20a=10a
Rearranging gives:
600=30a
Thus:
a=60030=20m/s2
Substitute the value of acceleration back into equation (2):
T=20a=20×20=400N
- The forces acting on B are:
- Applied force (F) = 600 N (to the right)
- Tension in the string (T) (to the left)
600−T=mB⋅a(3)
Substituting the values:
600−T=20a(3)
- The only force acting on A is the tension (T) in the string.
T=mA⋅a(4)
Substituting the values:
T=10a(4)
From equation (3):
600−T=20a
Substitute equation (4) into this:
600−10a=20a
Rearranging gives:
600=30a
Thus:
a=60030=20m/s2
Substitute the value of acceleration back into equation (4):
T=10a=10×20=200N
- Tension when the force is applied to A: 400 N
- Tension when the force is applied to B: 200 N
Topper's Solved these Questions
- LAWS OF MOTION Book:NCERT ENGLISHChapter:LAWS OF MOTION Exercise:EXERCISE
Explore 40 Videos
- KINETIC THEORYBook:NCERT ENGLISHChapter:KINETIC THEORYExercise:EXERCISE
Explore 14 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:EXERCISE
Explore 31 Videos
Similar Questions
Two bodies A and B of masses 10kg and 15kg respectively kept on a smooth, horizontal surface are tied to the ends of a light string. If T represents the tension in the string when a horizontal force F=500N is applied to A (as shown in figure 1) and T' be the tension when it is applied to B (figure2), then which of the following is true?

View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.

 .
.
View Solution
Knowledge Check
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400N
Two masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is

View SolutionThree block of masses m1=10kg,m2=20kg and m3=30kg are on a smooth horizontal table ,connected to each other by light horizontal string. A horizontal placed force F=60N is applied to m3, towards right find
(a) tensionT1 and T2 and
(b) tensionT2 if all of a sudden the string between m1 and m2 snaps.

View SolutionTwo balls of masses m1=5kg,m2=10kg are connected by a light inextensible string. A horizontal force F = 15 N is acting on the ball m2 along the line joining two balls as shown. What is the (a) acceleration of the balls (b) tension in the string?

View SolutionThere blocks a,b and c of massses 10 kg ,10 kg and 20 kg respectivaly are arrenged as shown in figure all the surface are frictionless and string is inextensible A constant force F= 20N is applied on block a as shown . pulley and string are light . part of the string connecting both pulleys is vertical and part of the string connecting pulleys with masses a and b are horizontal .
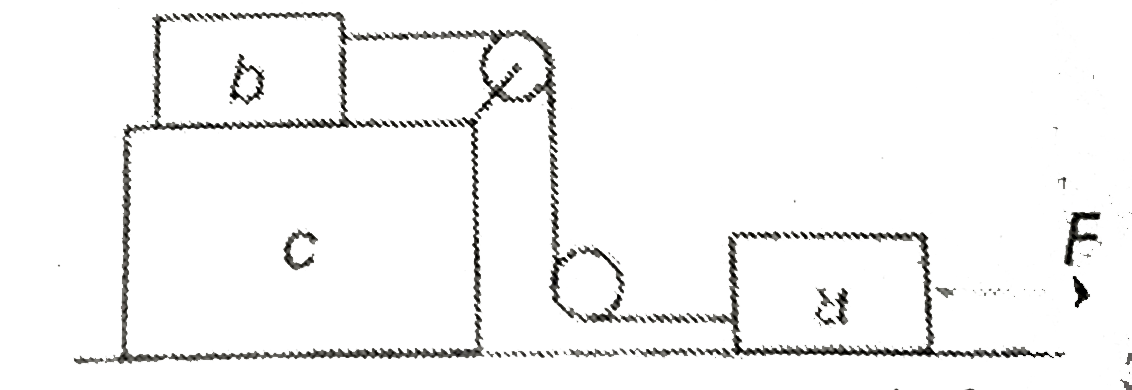
View SolutionTwo block of mass 1kg and 2kg are connected by a string AB of mass 1kg. The blocks are placed on a smooth horizontal surface. Block of mass 1kg is pulled by a horizontal force F of magnitude 8N. Find the tension in the string at points A and B

View SolutionTwo bodies of masses 4 kg and 6 kg connected by means of a light string are lying on a smooth horizontal surface. A horizontal pulling force is applied on the lighter body. Two seconds later the string connecting the two masses is cut. After two more seconds if the velocity of the heavier mass is 2ms−1, the force initially applied is
View SolutionA block of mass 10 kg lying on a smooth horizontal surface is being pulled by means of-a rope of mass 2 kg. If a force of 36N is applied at the end of the rope, the tension at the mid point of the rope is,
View Solution