A nucleus is at rest in the laboratory frame of reference. Show that if it disintegrates into two smaller nuclei the products must be emitted in opposite directions.
To solve the problem of showing that a nucleus at rest disintegrates into two smaller nuclei emitted in opposite directions, we can follow these steps:
1. Understand the Initial Condition:
- We start with a nucleus (mass M) that is at rest in the laboratory frame of reference. This means that its initial momentum is zero.
2. Define the Disintegration:
- When the nucleus disintegrates, it produces two smaller nuclei with masses m1 and m2. Let their velocities be →v1 and →v2 respectively.
3. Apply Conservation of Momentum:
- According to the law of conservation of momentum, the total momentum before disintegration must equal the total momentum after disintegration.
- The initial momentum Pi is:
Pi=0
- The final momentum Pf after disintegration is:
Pf=m1→v1+m2→v2
- Setting the initial momentum equal to the final momentum gives us:
0=m1→v1+m2→v2
4. Rearranging the Equation:
- From the equation m1→v1+m2→v2=0, we can rearrange it to express →v1 in terms of →v2:
m1→v1=−m2→v2
- Dividing both sides by m1:
→v1=−m2m1→v2
5. Interpret the Result:
- The negative sign in the equation →v1=−m2m1→v2 indicates that the velocities →v1 and →v2 are in opposite directions.
- Therefore, if one nucleus moves in one direction, the other nucleus must move in the opposite direction.
6. Conclusion:
- Hence, we have shown that when a nucleus at rest disintegrates into two smaller nuclei, the products must be emitted in opposite directions.
- We start with a nucleus (mass M) that is at rest in the laboratory frame of reference. This means that its initial momentum is zero.
- When the nucleus disintegrates, it produces two smaller nuclei with masses m1 and m2. Let their velocities be →v1 and →v2 respectively.
- According to the law of conservation of momentum, the total momentum before disintegration must equal the total momentum after disintegration.
- The initial momentum Pi is:
Pi=0
- The final momentum Pf after disintegration is:
Pf=m1→v1+m2→v2
- Setting the initial momentum equal to the final momentum gives us:
0=m1→v1+m2→v2
- From the equation m1→v1+m2→v2=0, we can rearrange it to express →v1 in terms of →v2:
m1→v1=−m2→v2
- Dividing both sides by m1:
→v1=−m2m1→v2
- The negative sign in the equation →v1=−m2m1→v2 indicates that the velocities →v1 and →v2 are in opposite directions.
- Therefore, if one nucleus moves in one direction, the other nucleus must move in the opposite direction.
- Hence, we have shown that when a nucleus at rest disintegrates into two smaller nuclei, the products must be emitted in opposite directions.
Topper's Solved these Questions
Similar Questions
Assertion: Stationary waves are so called because particles are at rest in stationary waves.
Reason: They are formed by the superposition of two identical waves travelling in opposite directions.
View SolutionA nucleus A, With a finite de-broglie wavelength λA, undergoes spontaneous fission into two nuclei B and C of equal mass. B flies in the same direction as that of A, While C flies in the opposite direction with a velocity equal to half of that of B . The de-Broglie wavelength λB and λB and C are respectively:
View SolutionA particular type of nucleus whose decay constant is λ is produced at a steady rate of p nuclei per second. Show that the number of nuclei N present t second after the production starts is N=Pλ[1−e~λt].
View SolutionAn isolated nucleus which was initially at rest, disintegrates into two nuclei due to internal nuclear forces and no γ rays are produced. If the ratio of their kinetic energy is found to be 6427, then
View SolutionH2 molecule has two electrons and two nuclei. In which form of hydrogen the spin of electrons and also the spin of nuclei are in opposite directions.
View SolutionTwo satellites A and B of equal mass move in the equatorial plane of the earth, close to earth's surface. Satellite A moves in the same direction as the of the rotation of the earth while satellite B moves in the opposite direction. Calclate the ratio of the kinetic energy of B of that of A in the reference frame fixed to the earth (g=9.8ms−2 and radius of the earth =6.37×106km)
View SolutionTwo satellites A and B of equal mass move in the equatorial plane of the earth, close to earth's surface. Satellite A moves in the same direction as the of the rotation of the earth while satellite B moves in the opposite direction. Calclate the ratio of the kinetic energy of B of that of A in the reference frame fixed to the earth (g=9.8ms−2 and radius of the earth =6.37×106m)
View SolutionA particle of mass 4m which is at rest explodes into masses m,m & 2m. Two of the fragments of masses m and 2m are found to move with equal speeds v each in opposite directions. The total mechanical energy released in the process of explosion is :-
View SolutionTwo blocks of masses m and 3m on a horizontal surface are in contact with the ends of a horizontal massless spring. The coefficient of friction between m and surface and between 3m and surface is μ and μ/3 respectively. The two blocks are moved towards each other to compress the spring and then released. The two blocks move off in opposite directions covering distances S1 and S2 before comming to rest. S1:S2 is
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
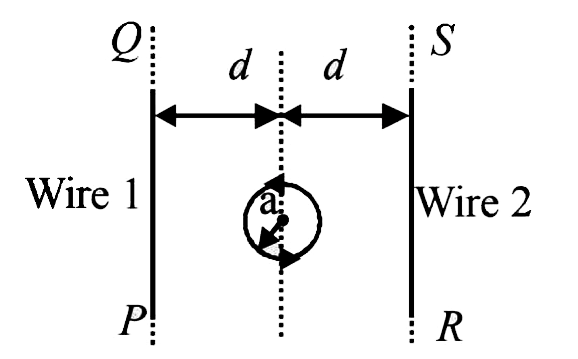
(5) Consider d>>a, and the loop is rotated about its diameter parallel to the wires by 30∘ from the position shown in the figure. If the currents in the wire are in the opposite directions, the torque on the loop at its new position will be ( assume that the net field due to the wires is constant over the loop).
View Solution
