A motor car is moving with a velocity of 108km/h and it takes 4second to stop after the brakes are applied. Calculate the force exerted by the brakes on the motorcar if its mass along with the passenger is 1000kg.
To solve the problem, we will follow these steps:
Step 1: Convert the velocity from km/h to m/s
The initial velocity of the motor car is given as 108km/h. We need to convert this to meters per second (m/s).
Velocity in m/s=Velocity in km/h×10003600
Substituting the value:
Velocity in m/s=108×10003600=30m/s
Step 2: Identify the final velocity
The final velocity of the car after it comes to a stop is 0m/s.
Step 3: Calculate the acceleration
We can find the acceleration using the formula:
a=vf−vit
Where:
- vf = final velocity = 0m/s
- vi = initial velocity = 30m/s
- t = time taken to stop = 4s
Substituting the values:
a=0−304=−304=−7.5m/s2
Step 4: Calculate the force exerted by the brakes
Using Newton's second law of motion, the force can be calculated as:
F=m⋅a
Where:
- m = mass of the car = 1000kg
- a = acceleration = −7.5m/s2
Substituting the values:
F=1000⋅(−7.5)=−7500N
Step 5: Interpret the result
The negative sign indicates that the force exerted by the brakes is in the opposite direction to the motion of the car, which is expected as brakes are meant to stop the vehicle.
Final Answer:
The force exerted by the brakes on the motor car is −7500N.
---
The initial velocity of the motor car is given as 108km/h. We need to convert this to meters per second (m/s).
The final velocity of the car after it comes to a stop is 0m/s.
We can find the acceleration using the formula:
- vf = final velocity = 0m/s
- vi = initial velocity = 30m/s
- t = time taken to stop = 4s
Using Newton's second law of motion, the force can be calculated as:
- m = mass of the car = 1000kg
- a = acceleration = −7.5m/s2
The negative sign indicates that the force exerted by the brakes is in the opposite direction to the motion of the car, which is expected as brakes are meant to stop the vehicle.
The force exerted by the brakes on the motor car is −7500N.
Topper's Solved these Questions
Similar Questions
A car of mass 480 kg moving at a speed of 54 km per hour is stopped in 10 s. Calculate the force applied by the brakes.
View SolutionA car of mass 800 kg is moving with a constant velocity 40 km/h. Find the net force on it.
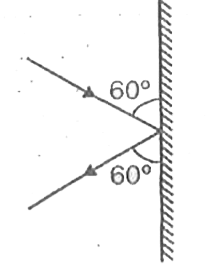
View SolutionA body of mass 3 kg moving with velocity 10 m/s hits a wall at an angle of 60∘ and returns at the same angle. The impact time was 0.2 s. Calculate the force exerted on the wall.
View SolutionA car of mass 800 kg is moving with a constant velocity 40 km/h . Find the net force on it.
View SolutionA car moving with a velocity of 40 km/h can be stopped by brekes after travelling at least 5 m. If same car moves at a speed of 80 km/h the minimum stopping distance is
View SolutionA bullet of mass 0.04 kg moving with a speed of 600 m/s penetrates a heavy wooden block. It stops after a penetration of 500 cm. The resistive force exerted by the block on the bullet is
View SolutionA car is moving with a uniform velocity 30ms−1 . It is stopped in 2 s by applying a force of 1500 N through its brakes.
Calculate the following values: The mass of car.
View SolutionThe distance travelled by a motor car in t second after the brakes are applied is s feet, where s = 22t −12t2. The distance travelled by the car before it stops, is
View SolutionA car is moving with a velocity 20m s−1. The brakes are applied to retard it at a rate of 2m s2. What will be the velocity after 5 s of applying the brakes?
View SolutionA car is moving with a velocity 20 m s−1. The brakes are applied to retard it at a rate of 2 m s−2. What will be the velocity after 5 s of applying the brakes ?.
View Solution
