A man of height 1.47 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road a =1.5×10−6/m. What is the apparent length of the road man is able to sec?
700m
2000 m
7000√2
infinite distance
The correct Answer is:B
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
2 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -II (ADVANCED) INTEGER TYPE QUESTIONS)
2 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE II LEVEL -I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
17 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
98 Videos
Similar Questions
A man of height 1.47 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road a =1.5×10−6/m. What is the apparent length of the road man is able to sec?
View SolutionA man of height 2 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road and a=2×10−6/m. What is the actual length of the road, man is able to see
View Solution
Knowledge Check
A man of height 2 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road and a=2×10−6/m. What is the actual length of the road, man is able to see
A2000mB390mCinfinite distanceDNone of these
What is the refractive index in a medium where the speed of light is 1.5×108 m/s ?
View SolutionA man of height 2.0m is standing on a level road because of temprature variation the refractive index of air is varying as μ=√1+ay, where y is height from road. If a=2.0×10−6m−1. Then, find distant point that he can see on the road.
View SolutionA man of height 2.0m is standing on a level road because of temprature variation the refractive index of air is varying as μ=√1+ay, where y is height from road. If a=2.0×10−6m−1. Then, find distant point that he can see on the road.
View SolutionOn a hot summer day in a desert the refractive index of the atmosphere changes with height (y) above the surface of the earth as μ=m0(1+by)1/2 where m0 is the refractive index at the surface and b=6×x10−4m−1. A man of height 1.5 m is standing on a straight level road. Calculate the distance beyond which he cannot see a point on the road.
View SolutionDue to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as n=n0√1+ay, where n0 is the index of refraction at the surface and a=2.0×10−6m−1 . A person of height h=2.0m stands on a level surface. Beyond what distance will he not see the runway?

View SolutionDue to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as n=n0√1+ay, where n0 is the index of refraction at the surface and a=2.0×10−6m−1 . A person of height h=2.0m stands on a level surface. Beyond what distance will he not see the runway?

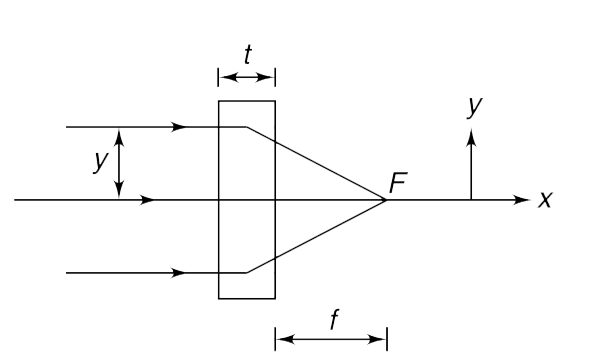
View SolutionA parallel beam of light travelling in x direction is incident on a glass slab of thickness t. The refractive index of the slab changes with y as μ=μ0(1–y2y02)where μ0 is the refractive index along x axis and y0 is a constant. The light beam gets focused at a point F on the x axis. By using the concept of optical path length calculate the focal length f. Assumef>>t and consider y to be small.
View Solution
