If AD and PM are median of triangles ABC and PQR respectively where ΔABC−ΔPQR, prove that ABPQ=ADPM.Solution in Kannada
Step by step video & image solution for If AD and PM are median of triangles ABC and PQR respectively where Delta ABC - Delta PQR, prove that (AB)/(PQ) = (AD)/(PM). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - ZEN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TEXTUAL EXERCISES (EXERCISE 2.4)
9 Videos
- TRIANGLESBOOK - ZEN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TEXTUAL EXERCISES (EXERCISE 2.5)
17 Videos
- TRIANGLESBOOK - ZEN PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TEXTUAL EXERCISES (EXERCISE 2.2)
9 Videos
- SURFACE AREAS AND VOLUMESBOOK - ZEN PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - ZEE ADDITIONAL QUESTIONS -HOTS [HIGHER ORDER THINKING SKILLS]-QUESTIONS
11 Videos
Similar Questions
Let ΔABC~ΔDEF and their areas be , respectively , 64cm2and121cm2 . If EF = 15.4 cm, find BC
View SolutionSides of triangles are given below. Determine which of them are right triangles.
In case of a right triangle , write the length of its hypotenuse.
7cm, 24 cm, 25 cm
View SolutionE and F are points on the sides PQ and PR respectively of a ΔPQR. For the following cases, state whether EF||QR.

i] PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm, and FR = 2.4 cm.
ii] PE = 4 cm, QE = 4.5 cm, PF = 8 cm, RF = 9 cm
iii] PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm, and PF = 0.36 cm.
View SolutionA sector of a circular is of radius 12 cm and angle 120∘. It is rolled up so that two bounding radii are joined together to form a cone. Find the volume of the cone.
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionAD और PM त्रिभुजों ABC और PQR कि क्रमशः मध्यिकाएँ है जबकि ΔABC~ΔPQR है सिद्ध कीजिए कि ABPQ=ADPM है
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that ΔABC~DetlaPQR
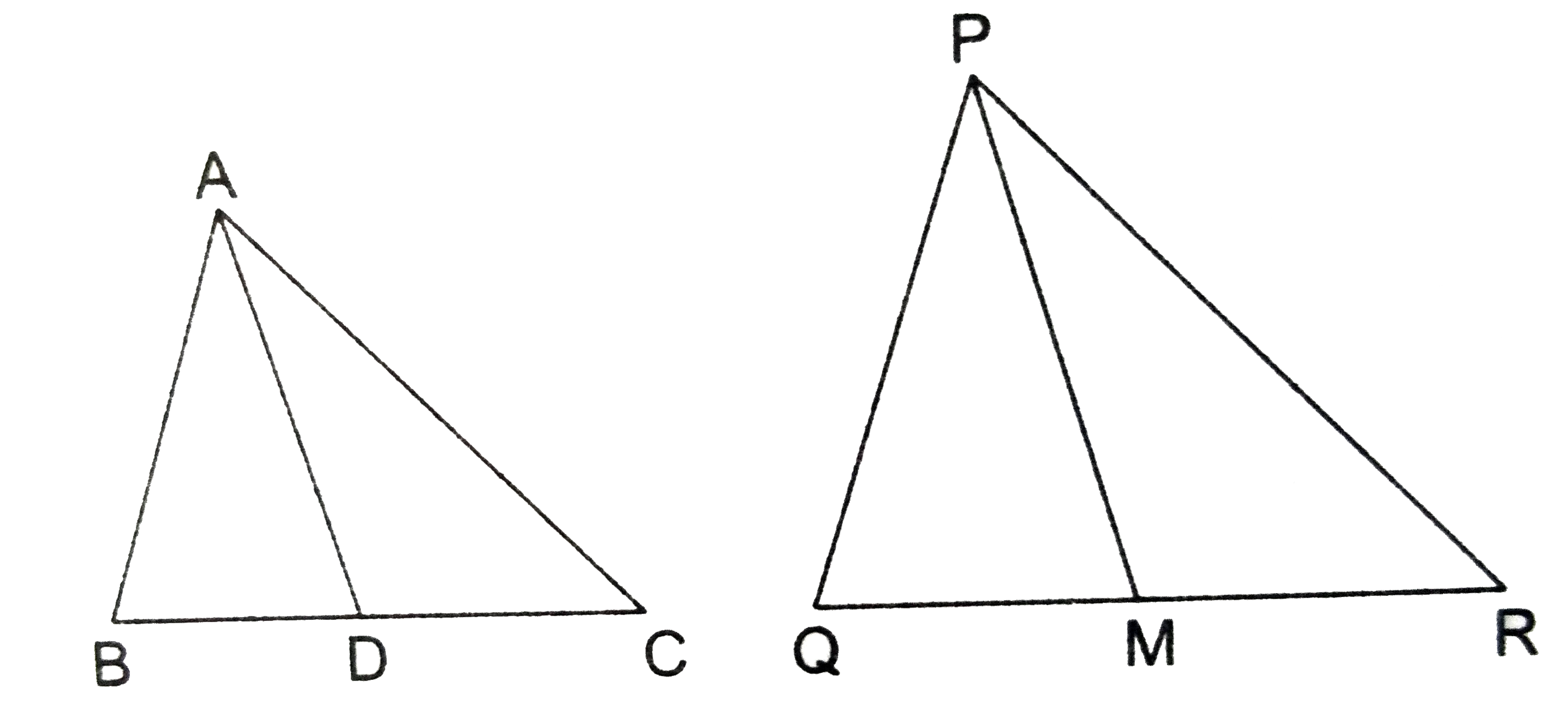
View Solutionएक त्रिभुज ABC की भुजाएं AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती है। दर्शाइए कि ΔABC~ΔPQR है।
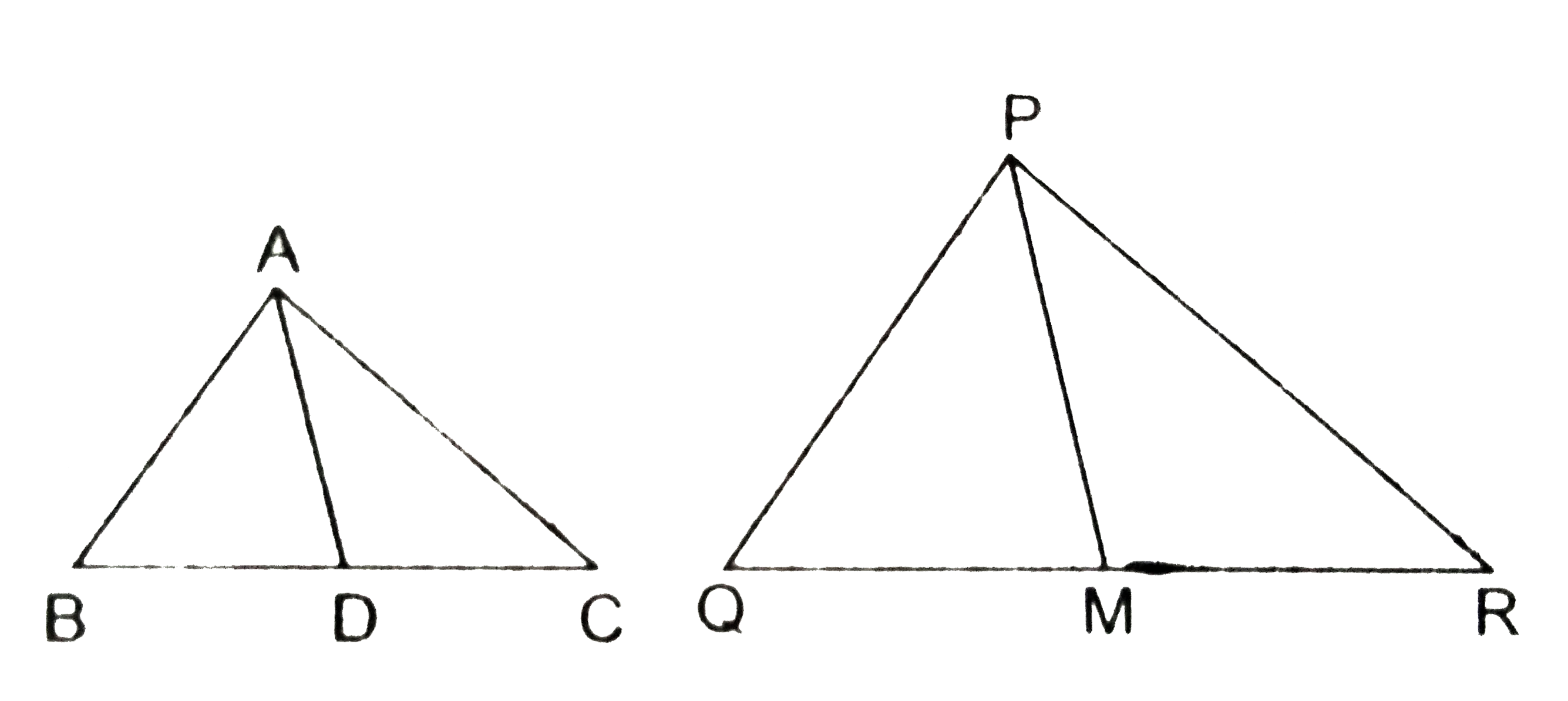
View SolutionAD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं , जबकि ΔABC~ΔPQR है । सिद्ध कीजिए कि ABPQ=ADPM है ।
View SolutionAD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं , जबकि ΔABC~ΔPQR है । सिद्ध कीजिए कि ABPQ=ADPM है ।
View Solutionयदि AD तथा PM क्रमशः △ABC तथा △PQR के समद्विभाजक है जहाँ △ABC~△PQR है तो सिद्ध कीजिए कि :
(i) ABPQ=ADPM
(ii) ∠ADC=∠PMR
View Solutionयदि AD और PM ΔABCऔरΔPQR की क्रमशः मध्यिकाएँ है , और जहाँ ΔABC~ΔPQR सिद्ध करें कि
(i) ABPQ=ADPM
(ii) ∠ADC=∠PMR
View SolutionIf Adand PM are medians of triangles ABC and PQR, respectively where ΔABC~ΔPQR , prove that ABPQ=ADPM
View SolutionIf AD and PM are median of triangles ABC and PQR respectively where ΔABC−ΔPQR, prove that ABPQ=ADPM.
View SolutionIf AD and PM are medians of triangles ABC and PQR respectively , where ΔABC~ΔPQR, prove that ABPQ=ADPM.
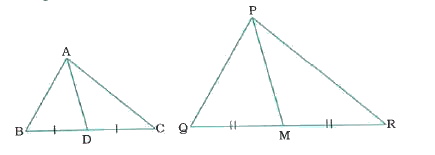
View SolutionSides AB and AC and median AD of a triangle ABC are proportional to sides PQ and PR and median PM of another triangle PQR. Prove that △ABC−△PQR .
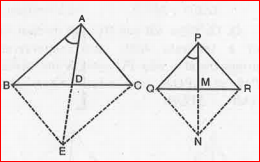 .
.
View Solution