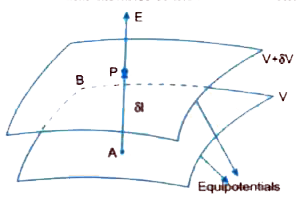
Two closely spaced equipotential surfaces A and B with potentials V and $V + δ V$ (where SV is the change in V) are kept 8l distance apart as shown in the Fig. Deduce the relation between the electric field and the potential gradient between them. Write the two important conclusions concerning the relation between the electric field and the electric potential.

Text Solution

Verified by Experts

Consider two closely spaced equipotential surfaces A and B, having uniform potentials V and V + $δ V$ in the direction of the electric field E. Let $δ l$ be the perpendicular distance of the surface A from a point P on surface B.
If we consider that a unit +ve charge is moved along this perpendicular from surface B to surface A against the electric field then work done
$δ W = E δ I$
By definition the work done equals the potential difference
$(V_{A} - V_{B}) = V - (V + δ V) = δ V$
$\Rightarrow E δ I = - δ V or E = - \frac{δ V}{δ I} (or - \frac{d V}{d l})$
For two important conclusions.

Updated on:21/07/2023

The correct relation between electric intensity E and electric potential V is
A $E = - \frac{d V}{d r}$
B $E = \frac{d V}{d r}$
C $V = - \frac{d E}{d r}$
D $V = \frac{d E}{d r}$
What do you understand by potential gradient ?
Establish a relation between electric field and potential gradient.
AElectric field is in the direction in which the potential decreases steepest
BMagnitude of electric field is given by the charge in the magnitude of potential per unit displacement jnormal to the equipotential surface at the point.
CIn the region of strong electrric field, equipotential surfaces are far apart.
DBoth the statements (a) and (b) are correct.
In the region where electric field $E = 0$ , the relation between electirc potential $V$ and distance $r$ is
A $V \propto r$
B $V \propto 1 / r$
C $V \propto r^{2}$
D $V =$ constant