Figure shows two idential capacitors, C1andC2, each of 1μF capacitance connected to a battery of 6 V. Initially switch 'S' is closed. After sometime 'S' is left open and dielectric slabs of dielectric constant K = 3 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?

Initially,when the switch S is closed in the arrangment shown, we have
C1=C2=1μF,V1=V2=6VandQ1=Q2=CV=6μF
When the switch S is left open, the capacitor C1 is still connected to the battery but capacitor C2 is now disconnected from the battery.
On inserting dielectric slabs of dielectric constant K = 3, so as to fill completely the space between the plates of two capacitors,their capacity changes to C.1=C.2=KC1orKC2=3×1μF=3μF
(i) As capacitor C1 is still connected to the battery, its new voltage V.1=V1=6V and new charge Q.1=C.1V.1=3μF×6V=18μC
(ii) As capacitor C2 is now disconnected from the battery, its new charge Q.2=Q2=6μC and new potential difference across its plates
V.2=Q.2C.2=6μC3μF=2V.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - LONG ANSWER QUESTIONS-I
64 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - LONG ANSWER QUESTIONS-II
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - VERY SHORT ANSWER QUESTIONS
40 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
Figure shows two identical capacitors C1andC2 each of 2μF capacitance, connected to a battery of 5 V. Initially switch 'S' is closed. After some time 'S' is left open and dielectric slavs of dielectric constant K = 5 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?
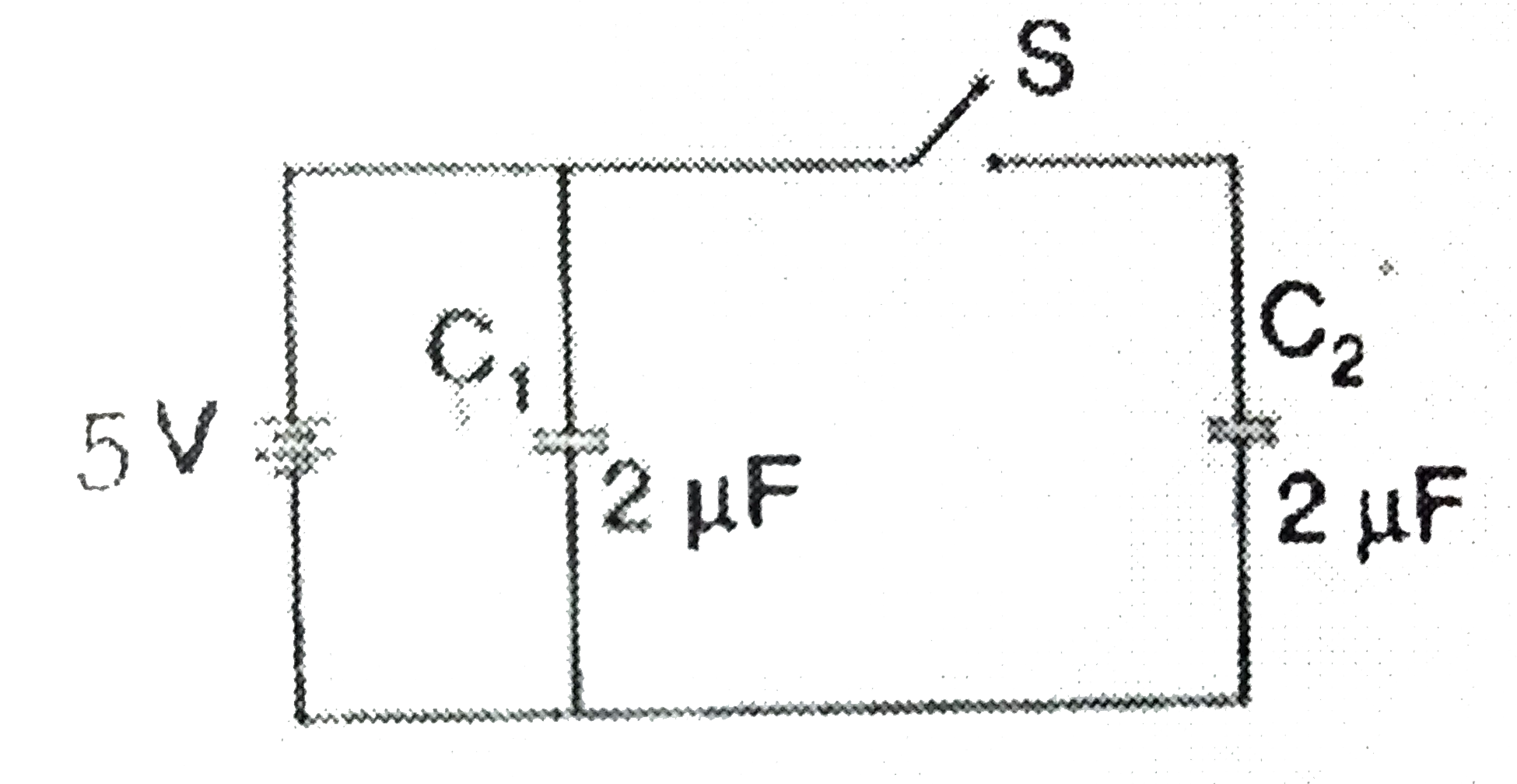
View SolutionFigure shows two identical capacitors C1andC2 each of 2μF capacitance, connected to a battery of 5 V. Initially switch 'S' is closed. After some time 'S' is left open and dielectric slavs of dielectric constant K = 5 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?

View Solution
Knowledge Check
A capacitor plates are charged by a battery with ‘V’ volts. After charging battery is disconnected and a dielectric slab with dielectric constant ‘K’ is inserted between its plates, the potential across the plates of a capacitor will become
AZeroBV2CVkDKV
Figure shows two identical caoacitors C1andC2 each of 1.5μF caoacitance, connected to a battery of 2 V. Initially switch 'S' is closed. After some time 's' is left open and dielectric slabs of dielectric constant K=2 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted.
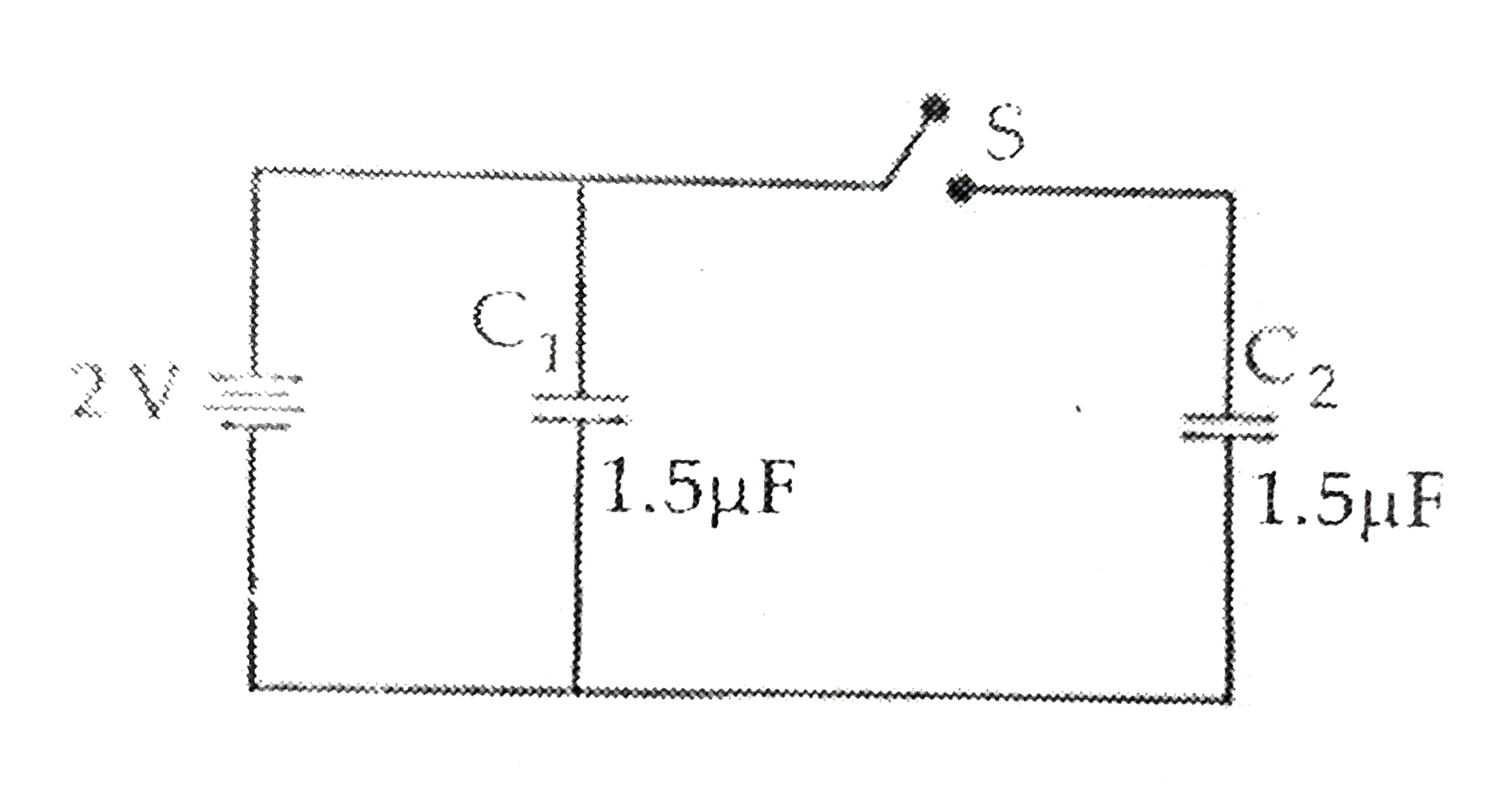
View SolutionFigure shows two identical caoacitors C1andC2 each of 1.5μF caoacitance, connected to a battery of 2 V. Initially switch 'S' is closed. After some time 's' is left open and dielectric slabs of dielectric constant K=2 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted.

View SolutionFig. shows two identical capacitors C1andC2 each of 1μF capacitance, connected to a battery of 6V Initially,swich S is closed. After sometime, S is left open and dielectric slabs of dielectric constant K = 3 are instered to fill compelelty the space between the plates of two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after teh slabs are inserted ?
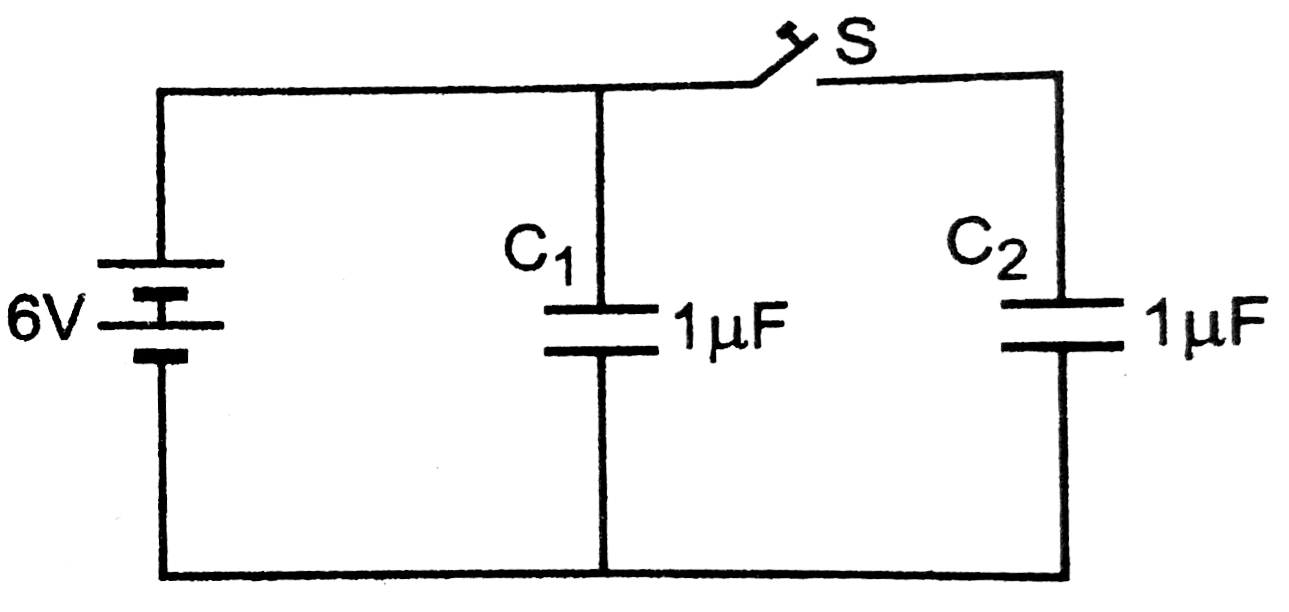
View SolutionFig, shows two indentical capacitors C1andC2 each of 1uF capacitance connected to a battery of 6V. Initially, swich S is closed. After some time, the swich S is left open and dielectric slabs of K = 3 are inserted to filll completely the space between the plates of two capacitors . How will (i) the charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted ?
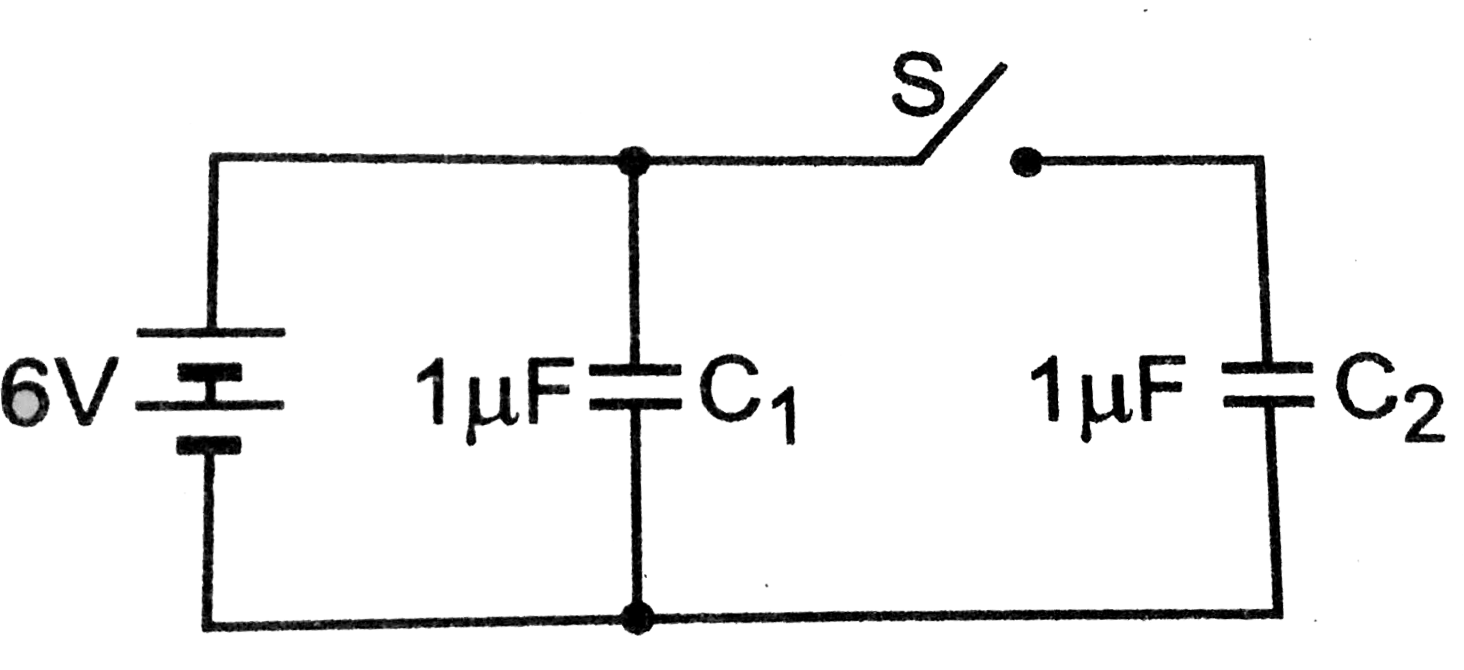
View SolutionFig, shows two indentical capacitors C1andC2 each of 1μF capacitance connected to a battery of 6V. Inditally, swich S is closed. After some time, the swich S is left open and dielectric slabs of K = 3 are inserted to filll completely the space between the plates of two capacitors . How will (i) the charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted ?

View SolutionTwo dielectric slabs of dielectric constants K1andK2 are filled in between the two plates, each of area A, of the parallel plate capacitor as shown in the figure. Find the net capacitance of the capacitor.

View SolutionTwo dielectric slabs of constant K1 and K2 have been filled in between the plates of a capacitor as shown below. What will be the capacitance of the capacitor
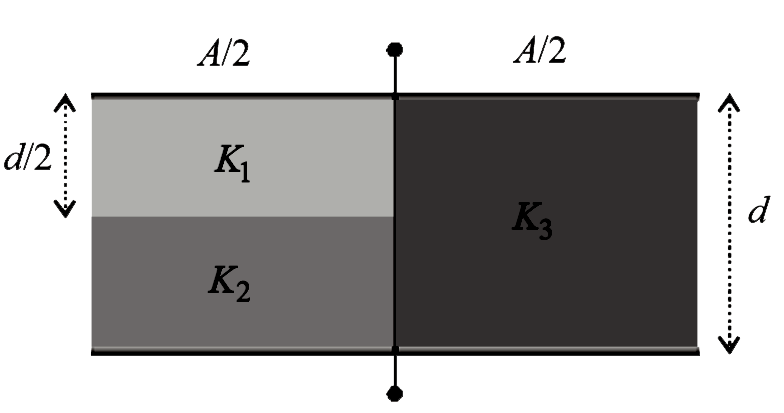
View Solution
