In a quark model of elementary particles, a neutron is made of one up quark (charge =23e) and two down quarks (charges =13e). Assume that they have a triangle configuration with side length of the order of 10−15m. Calculate electrostatic potential energy of neutron.
The electrostatic potential energy of neutron
u=14πε0⎡⎢
⎢⎣(23e)(−13e)r+(23e)(−13e)r+(−13e)(−13e)r⎤⎥
⎥⎦
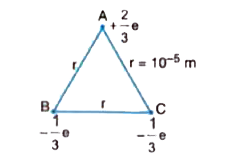
14πε0(−13e2r)=−9×109×(1.6×10−19)23×(10−15)
=−7.68×10−14J=−7.68×10−141.6×10−19eV=−4.8×105eV=−0.48MeV
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - LONG ANSWER QUESTIONS-I
64 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - LONG ANSWER QUESTIONS-II
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - VERY SHORT ANSWER QUESTIONS
40 Videos
- ELECTROMAGNETICE INDUCTIONBOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D
1 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
Similar Questions
(a) In a quark model of elementary particles, a neutron is made of one up quarks [charge (2/3)e] and two down quarks [charges - (1/3)e].As∑etˆtheyhavea△configurationwiths≤n>hoftheorderof10^(-15) m. Calculate electrostatic potential energy of neutron and compare it with its mass 939 MeV.
(b) Repeat above exercise for a proton which is made of two up and one down quark.

View SolutionTwo point charges of 10 C each are kept at a distance of 3 m in vacuum. Calculate their electrostatic potential energy.
View Solution
Knowledge Check
(a) In a quark model of elementary particles, a neutron is made of one up quarks [charge (2/3)e] and two down quarks [charges - (1/3)e]. Assume that they have a triangle configuration with side length of the order of 10−15m. Calculate electrostatic potential energy of neutron and compare it with its mass 939 MeV.
(b) Repeat above exercise for a proton which is made of two up and one down quark.
 A7.68B−5.21C−0.48D9.34
A7.68B−5.21C−0.48D9.34The neutron is a particle with zero charge still it has a non-zero magnetic moment with z-component 9.66×10−27A−m2. This can be explained by the internal structure of the neutron. The evidence indicates that a neutron is composed of three fundamental particles calleed quarks : an up (u) quark, of charge +2e3, and two down (d) quarks, each of change −e3. The combinations of the three quarks prodcues a net charge of 2e3−e3−e3=0.
_E01_154_Q01.png)
If the quarks are in motion they can produce a non-zero magnetic moment. As a very simple model, suppose the u quark moves in a counter clockwise circular path and the d quarks move in a clockwise circular path, all of the radius r and all with the same speed v see figure.
If all Quarks start moving in the same direction then what will be the magnetic moment of the neutron :-Aevr3πrB2evr3CevrDNone of theseThe neutron is a particle with zero charge still it has a non-zero magnetic moment with z-component 9.66×10−27A−m2. This can be explained by the internal structure of the neutron. The evidence indicates that a neutron is composed of three fundamental particles calleed quarks : an up (u) quark, of charge +2e3, and two down (d) quarks, each of change −e3. The combinations of the three quarks prodcues a net charge of 2e3−e3−e3=0.
_E01_152_Q01.png)
If the quarks are in motion they can produce a non-zero magnetic moment. As a very simple model, suppose the u quark moves in a counter clockwise circular path and the d quarks move in a clockwise circular path, all of the radius r and all with the same speed v see figure.
Determine the magnitude of the magnetic moment due of the circular u quark :-Aevr3πrB2evr3C4evr3Devr
Three charges +q,2qand−4q are placed on the three vertices of an equale-laterail triangle of each side0⋅1m. Calculate electrostatic potential energy of the system, take q=10−7C
View SolutionThree charges of 1 nC, 2 nC and 3 nC are placed at the corners of an equilateral triangle of side √3m. Calculate electrostatic potential at a point equidistant from the three corners of the triangle.
View SolutionThree point charges Q1=25μC,Q2=50μC and Q3=100μC, are kept at the corners A, B and C respectively of an equilateral triangle ABC having each side equal to 7.5 m. Calculate the total electrostatic potential energy of the system.
View SolutionThe neutron is a particle with zero charge still it has a non-zero magnetic moment with z-component 9.66×10−27A−m2. This can be explained by the internal structure of the neutron. The evidence indicates that a neutron is composed of three fundamental particles calleed quarks : an up (u) quark, of charge +2e3, and two down (d) quarks, each of change −e3. The combinations of the three quarks prodcues a net charge of 2e3−e3−e3=0.
_E01_151_Q01.png)
If the quarks are in motion they can produce a non-zero magnetic moment. As a very simple model, suppose the u quark moves in a counter clockwise circular path and the d quarks move in a clockwise circular path, all of the radius r and all with the same speed v see figure.
The current due to the circular motion of the u quark :-
View SolutionThe neutron is a particle with zero charge still it has a non-zero magnetic moment with z-component 9.66×10−27A−m2. This can be explained by the internal structure of the neutron. The evidence indicates that a neutron is composed of three fundamental particles calleed quarks : an up (u) quark, of charge +2e3, and two down (d) quarks, each of change −e3. The combinations of the three quarks prodcues a net charge of 2e3−e3−e3=0.
_E01_153_Q01.png)
If the quarks are in motion they can produce a non-zero magnetic moment. As a very simple model, suppose the u quark moves in a counter clockwise circular path and the d quarks move in a clockwise circular path, all of the radius r and all with the same speed v see figure.
Determine the magnitude of the three-quark system :-
View Solution
