The acceleration (a) of a particle depends on displacement (s) as a a=5+s . Initially s=0,v=5, then velocity v correspondig to the displacement is given by
v=5+s
v=√5+s
v=√s2+10s
v=s−5
The correct Answer is:A
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
79 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
91 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
91 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
The acceleration (a) of a particle depends on displacement (s) as a=5+s . Initially s=0,v=5, then velocity v corresponding to the displacement is given by
View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (s) as a=2s. The velocity of the particle is zero at zero displacement. Find the corresponding velocity-displacement equation.
View Solution
Knowledge Check
The acceleration of a particle depends on displacement covered in a time as a=s+5. It is given that initially s=0 and v=5m/s, then which of the following is possibly correct ?
Av=s+5Bv=√s+5Cv=loge(s+55)2Dv=loge(s+5s)The acceleration a of α of a particle depends on displacements covered in a time t as a=S+5 . It is given that initially S=0 m and v=5m/s. Then
Av=S+5Bv=√S+5Ct=loge(S+5S)Dt=loge(S+55)The acceleration of a particle is given by a = 3t and at t = 0, v = 0, x = 0. The velocity and displacement at t = 2 sec will be-
A6 m/s, 4 mB4 m/s, 6 mC3 m/s, 2 mD2 m/s, 3 m
The acceleration (a) of a particle moving in a straight line varies with its displacement (S) as a=2S. The velocity of the particle is zero and zero displacement. Find the corresponding velocity-displacement equation.
View SolutionThe acceleration of a particle is given by, a = t/6 at t = 0, velocity v = 2 m/s, displacement s= 2m. Find the velocity at t= 4 seconds,
View SolutionThe acceleration of particle varies with time as shown.
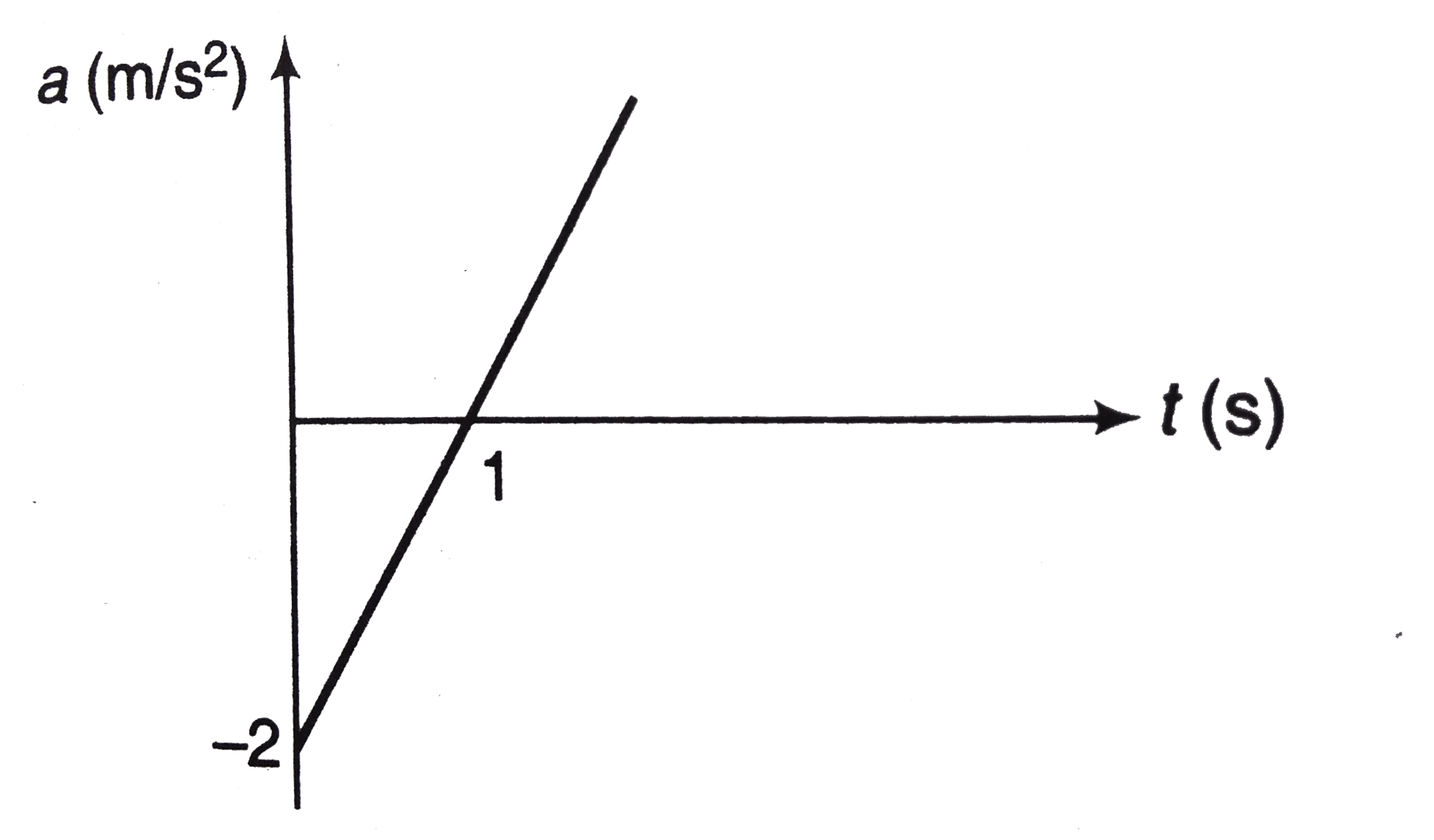
(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View Solution5.The displacement s of a particle at a time t is given by s= 2t - 5t + 4t - 3, find (i) the time when the acceleration is 14 ft/sec (ii)the velocity and the displacement at that time.
View Solution
