The acceleration (a) of a particle depends on displacement (s) as a=5+s . Initially s=0,v=5, then velocity v corresponding to the displacement is given by
A) v=5+s
B) v=√5+s
C) v=√s2+10s
D) v=s−5
The correct Answer is:A
To solve the problem, we need to find the velocity v as a function of displacement s given the relationship between acceleration a and displacement s.
1. Write the given equation for acceleration:
a=5+s
2. Relate acceleration to velocity:
We know that acceleration a can be expressed as:
a=dvdt
But we can also express it in terms of displacement s:
a=vdvds
Hence, we can write:
vdvds=5+s
3. Separate the variables:
Rearranging the equation gives:
vdv=(5+s)ds
4. Integrate both sides:
Now we integrate both sides:
∫vdv=∫(5+s)ds
The left side integrates to:
v22
The right side integrates to:
5s+s22+C
Thus, we have:
v22=5s+s22+C
5. Apply initial conditions:
We know that initially when s=0, v=5. Plugging these values into the equation:
522=5(0)+022+C
This simplifies to:
252=C
6. Substitute C back into the equation:
Now substituting C back into the equation gives:
v22=5s+s22+252
7. Multiply through by 2:
To eliminate the fraction, multiply the entire equation by 2:
v2=10s+s2+25
8. Rearrange the equation:
Rearranging gives:
v2=s2+10s+25
9. Factor the right-hand side:
The right-hand side can be factored as:
v2=(s+5)2
10. Take the square root:
Taking the square root of both sides gives:
v=s+5
Final Answer:
Thus, the velocity v corresponding to the displacement s is:
v=s+5
a=5+s
We know that acceleration a can be expressed as:
a=dvdt
But we can also express it in terms of displacement s:
a=vdvds
Hence, we can write:
vdvds=5+s
Rearranging the equation gives:
vdv=(5+s)ds
Now we integrate both sides:
∫vdv=∫(5+s)ds
The left side integrates to:
v22
The right side integrates to:
5s+s22+C
Thus, we have:
v22=5s+s22+C
We know that initially when s=0, v=5. Plugging these values into the equation:
522=5(0)+022+C
This simplifies to:
252=C
Now substituting C back into the equation gives:
v22=5s+s22+252
To eliminate the fraction, multiply the entire equation by 2:
v2=10s+s2+25
Rearranging gives:
v2=s2+10s+25
The right-hand side can be factored as:
v2=(s+5)2
Taking the square root of both sides gives:
v=s+5
Thus, the velocity v corresponding to the displacement s is:
v=s+5
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
The acceleration (a) of a particle moving in a straight line varies with its displacement (s) as a=2s. The velocity of the particle is zero at zero displacement. Find the corresponding velocity-displacement equation.
View SolutionThe acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
View SolutionThe velocity v and displacement x of a particle executing simple harmonic motion are related as
vdvdx=−ω2x.
Atx=0,v=v0. Find the velocity v when the displacement becomes x.
View SolutionThe velocity v and displacement x of a particle executing simple harmonic motion are related as
vdvdx=−ω2x.
Atx=0,v=v0. Find the velocity v when the displacement becomes x.
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View SolutionVelocity and acceleration of a particle at time t=0are u=(2ˆi+3ˆj)m/sanda=(4ˆi+3ˆj)m/s2 respectively. Find the velocity and displacement if particle at t=2s.
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
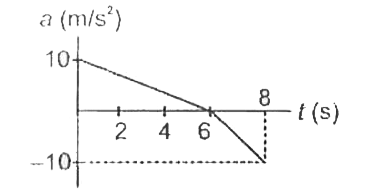
View SolutionIf acceleration of a particle at any time is given by a=2t+5
Calculate the velocity after 5 s, if it starts from rest
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
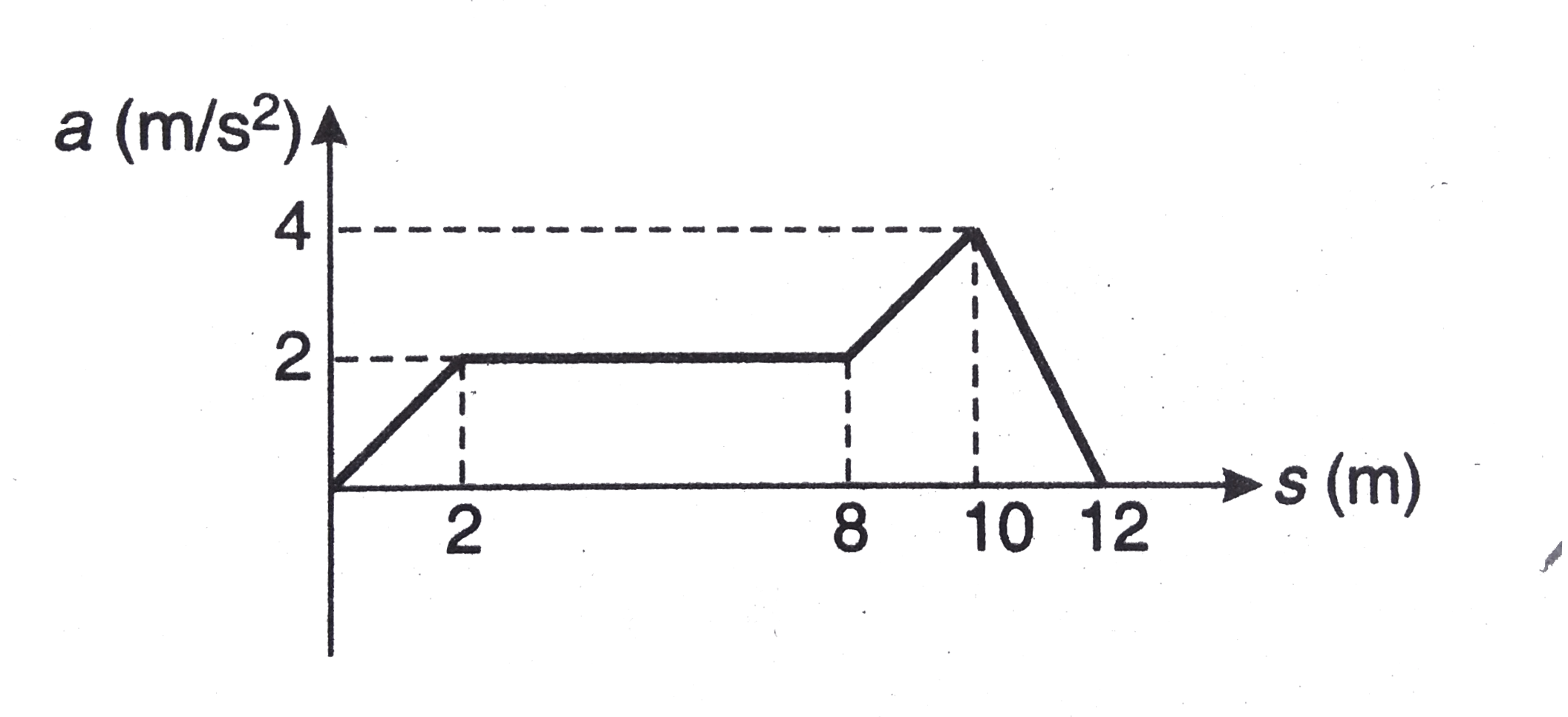
View SolutionVelocity of a particle at time t=0 is 2ˆi m/s. A constant acceleration of 2ms2 acts on the particle for 2s at an angle of 60∘ with its initial velocity. Find the magnitude of velocity and displacement of particle at the end of t=2s.
View Solution
