Question

Obtain the expression of electric field at any point by continuous distribution of charge on a volume.

Explanation

Suppose a continuous charge distribution in space has a charge density `rho`.
Choose any convenient origin O and let the position vector of any point in the charge distribution be `vecr`.

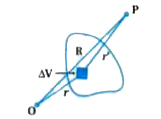
Divide the charge distribution into small volume elements of size `DeltaV`.
The charge in a volume element `DeltaV` is `rhoDeltaV`.
Now, consider any general point P (inside or outside the distribution with position vector `vecR`.
Electric field due to the charge `rhoDeltaV` is given by Coulomb.s law.
`vecE = sum(krhoDeltaV)/(r.)^(2).hatr`
where r. is the distance between the charge element and P and f. is a unit vector in the direction from the charge element to P.
By the superposition principle, the total electric field,
`vecE = int_(V) (krho.DeltaV)/(r.)^(2)hatr = k -= (rho DeltaV)/(r^(2)).hatr`
OR `vecE = kint(rho.DeltaV)/(r^(-2).hatr`
In short, using Coulomb.s law and the superposition principle, electric field can be determined for any charge distribution, discrete or continuous or part discrete and part continuous.