A circle, having radii 'a' has line charge distribution over its circumference having linear charge density λ=λ0cos2θ. Calculate the total electric charge residing on the circumference of the circle.
[Hint: ∫2π0cos2dθ=π] Solution in Gujrati
The length of an infinitesimally small lint element shown in fig. is add, then the charge or the line element is
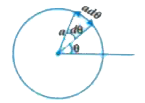
dq=λadθ(∴λ=ql)
∴dq=λ0cos2θ.dθ………(i)
(∴λ=λ0cos2θ)
In order to calculate the total charge Q residing on the surface, we have to intigrate dq over the entire surface
∴Q=∫2π0λ0cos2θ.dθ
=aλ0∫2π0cos2θ.dθ
∴Q=aλ0π (∴∫2π0cos2θdθ=π)
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION C NCERT EXEMPLAR SOLUTION (MULTIPLE CHOICE QUESTIONS (MCQs))7videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION C NCERT EXEMPLAR SOLUTION (MULTIPLE CHOICE QUESTIONS (MORE THAN ONE OPTION))6videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION B NUMERICALS (ADDITONAL EXERCISE)10videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section-D (MCQs asked in GUJCET/Board Exam)1videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )38videos
ELECTROMAGNETIC INDUCTION
Similar Questions
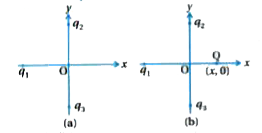
In figure, two positive charges q2 and q3 fixed along the y-axis, exert a net electric force in the + x direction on a charge q1 fixed along the x-axis. If a positive charge Q is added at (x, 0), the force on q1
 02:56View Solution
02:56View SolutionIf ∮s→E.→dS=0 over a surface, then
07:12View SolutionAn oil drop of 12 excess electrons is held stationary under a constant electric field of 2.55×104NC−1. (Millikan's oil drop experiment). The density of the oil is 1.26gcm−3. Estimate the radius of the drop, (g=9.81ms−2,e=1.60×10−19C).
08:57View SolutionMass of photon in motion is ………
02:53View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......
 03:25View Solution
03:25View SolutionCharge over a nonconducting ring is distributed so that the linear charge density varies as λ=λ0sinθ. What is the direction of force on a charge q0 placed at the center?
 01:16View Solution
01:16View SolutionA semicircular wire is uniformly charged with linear charge density dependent on the angle theta from y -direction as lambda=lambda_(0) |sin theta| , where lambda_(0) is a constant. The electric field intensity at the centre of the arc is
08:07View SolutionA thin non-conducting ring of radius R has a linear charge density lambda=lambda_(0) cos theta , where theta is measured as shown. The total electric dipole moment of the charge distribution is
03:59View SolutionThe linear charge density of a uniform semicircular wire varies with theta shown in the figure as lambda=lambda_(0)costheta if R is the radius of the loop ,of the charge on the wire is
04:23View SolutionA non conducting ring of radius R_(1) is charged such that the linear charge density is lambda_(1)cos^(2)theta where theta is the polar angle. If the radius is increased to R_(2) keeping the charge constant, the linear charge density is changed to lambda_(2)cos^(2)theta . The relation connecting R_(1) , R_(2)lambda_(1) and lambda_(2) will be
03:27View Solution∫π/20cos2θdθ=
05:23View SolutionCharge on the ring is given as lambda=lambda_(0)cos theta C/m .Find dipole moment of the ring
03:06View SolutionA circle of radius a has charge density given by lambda=lambda_(0)cos^(2)theta on its circumference, where lambda_(0) is a positive constant and theta is the angular position of a point on the circle with respect to some reference line. The potential at the centre of the circle is
03:47View SolutionA circle of radius 'a' has charge density given by λ=λ0cos2θ on its circumference. What will be the total charge on the circle ?
04:13View SolutionEvaluate the definite integrals .
π∫0√2+2cosθdθ03:21View Solution

