A cylinderical vessel is filled with water up to height H. A hole is bored in the wall at a depth h from the free surface of water. For maximum range h is equal to
H4
H2
3H4
H
The correct Answer is:B
Velocity of water flowing out of hole, v=√2gh
Height of hole from ground level =(H−h)
The time taken by water to cover vertical distance (H−h) is given by (H−h)=12gt2ort=√2(H−h)g
Horizontal range will be maximum if dRdh=0
i.e. 2×12(hH−h2)−1/2×(H−2h)=0
or H=2horh=H2
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Check Your Neet Vitals22videos
PROPERTIES OF BULK MATTER
- BOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)40videos
PROPERTIES OF BULK MATTER
- BOOK - MTG GUIDECHAPTER - PROPERTIES OF BULK MATTEREXERCISE - AIPMT/NEET (MCQs)40videos
PROPERTIES OF BULK MATTER
- BOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ14videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - MTG GUIDECHAPTER - THERMODYNAMICSEXERCISE - AIPMT/NEET (MCQs)26videos
THERMODYNAMICS
Similar Questions
A tank is filled with water to a height H. A hole is punched in the wall at a depth h below the water surface. Find the distance x from the wall at which the stream strikes the floor. Could a hole be punched at another depth so that this second stream would have the same range? If so at what depth? For what value of h is range maximum?
View SolutionA cylindrical vessel filled with water to a hight H. A vessel has two small holes in the side, from which water iins rushing out horizontal and the two steams stike the ground at the same poin, if the lower hole Q Q is h height above the ground, then the height of hole P above the ground will be
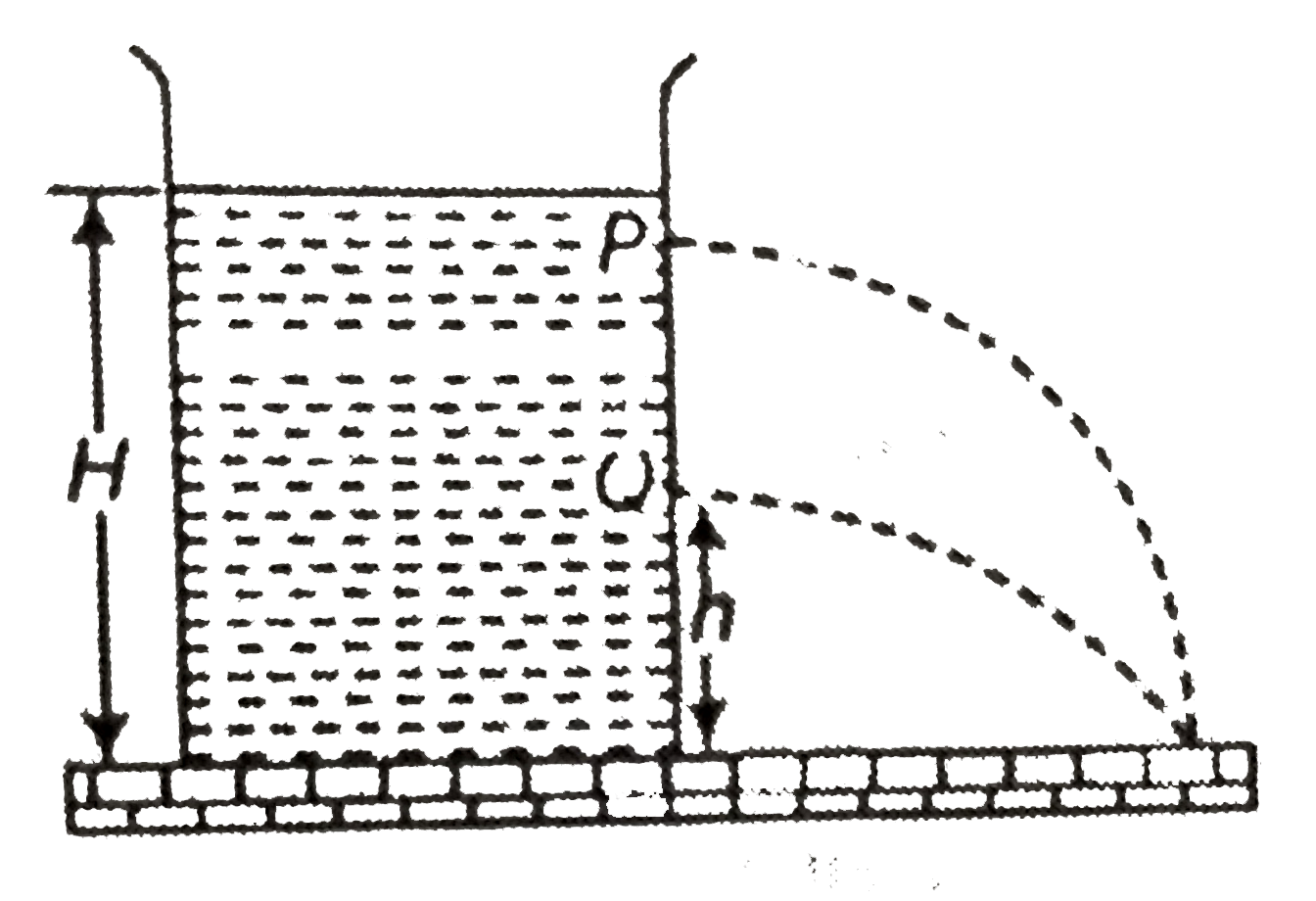 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
 Ax is equal if hole is at depth y or H-yBx is maximum for y=H/2CBoth (a ) and (b) are correctDBoth (d) and (d) are wrong
Ax is equal if hole is at depth y or H-yBx is maximum for y=H/2CBoth (a ) and (b) are correctDBoth (d) and (d) are wrong - Question 2 - Select One
A tank with vertical walls is mounted so that its base is at a height H above the horizontal ground. The tak is filled with water to a depth h. A hole is puched in the side wall of the tank at a depth x below the water surface. To have maximum range of the emerging stream, the value of x is
AH+h4BH+h2CH+h3D3(H+h)4 - Question 3 - Select One
A tank with vertical walls is monted so that its base is at height of 1.2 m above the horizotnal ground. The tank is filled with water to depth 2.8 m. A holw is punched in the side wall of the tank at a depth x m below the surface of water to have maximum range of the emerging stream. then the value of x in metre is
A4B1.6C2D2.3
A tank is filled with water up to a height H. Water is allowed to come out of a hole P in one of the walls at a depth D below the surface of water. Express the horizontal distance x in terms of H and D
 .View Solution
.View SolutionA tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
View SolutionA tank if filled with water upto height H. When a hole is made at a distance h below the level of water. What will be the horizontal range of water jet ?
View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
View Solution

