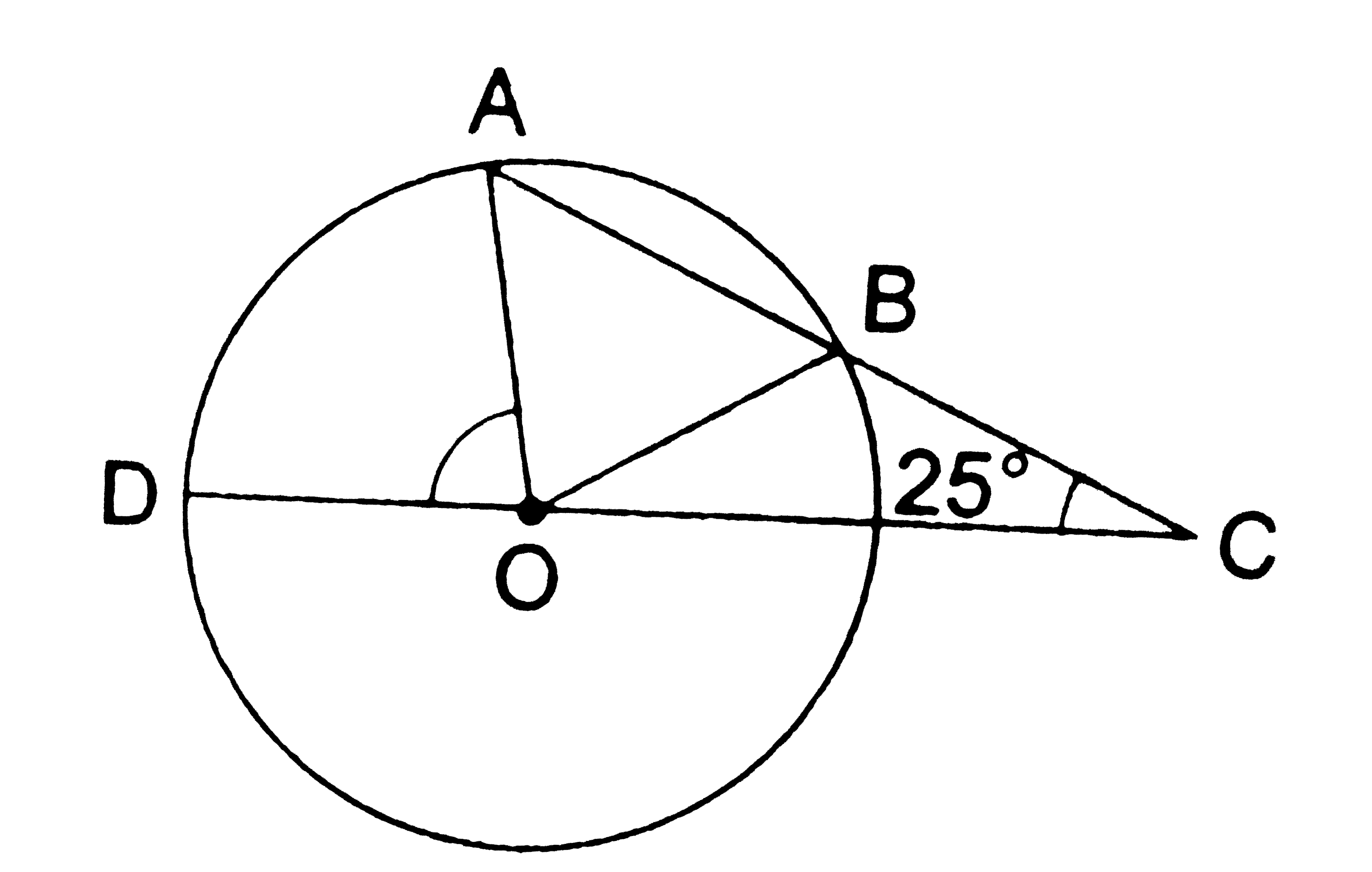
In the given figure, AB is a chrod of a circle with centre O and AB is produced to C such that BC = OB. Also, CO is joined and produced to meet the circle in D. If ∠ACD=25∘ then ∠AOD=?
50∘
75∘
90∘
100∘
The correct Answer is:B
OB=BC⇒∠BOC=∠BCO=25∘
Ext. ∠OBA=∠BOC+∠BCO=25∘+25∘=50∘
OA=OB⇒∠OAB=∠OBA=50∘
In ΔAOC, side CO has been produced to D.
∴ ext. ∠AOD=∠OAC+∠ACO=∠OAB+∠BCO=50∘+25∘=75∘
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)5videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B16videos
BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
Similar Questions
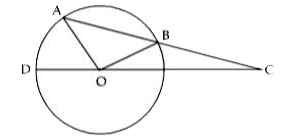
AB is the chord of a circle with centreO. AB is produced to C, such that BC =OB, CO is joined and produced to meet the circle in D.
If ∠ACD=Y∘ and ∠AOD=x∘, Prove that x=3y.View SolutionIn the figure given below, AB is the chord of a circle with centre O. AB is extended to C such that BC = OB. The straight line Co is produced to meet the circle at D. If ACD = y and AOD = x, such that x = ky, then the value of k is.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
AB is a chord in a circle with centre O. AB is produced to C such that BC is equal to the radius of the circle. C is joined to O and produced to meet the circle at D. If ∠ACD=32∘, then the measure of ∠AOD is .......
A48∘B96∘C108∘D80∘ - Question 2 - Select One
In the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
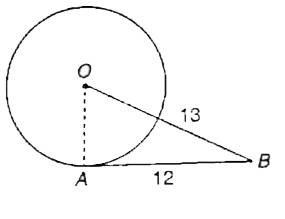 A6.5 cmB6 cmC5 cmDnone of these
A6.5 cmB6 cmC5 cmDnone of these
In the figure given below, AD is a diameter of a circle with centre O.If AB ll CD, prove that AB=CD
View SolutionIn the given figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisectors of ∠BAC.
View SolutionIn the figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionIn the figure, ACDB is a chord cutting two concentric circles with centre O. Find AB if CD = 8 cm, OD = 5 cm, and OB = 9 cm.
View SolutionIn the Figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD
View SolutionIn the given fig, AB is the diameter of the circle with centre O. The point C, D and E are on the circle such that AC = CD = DE = EB. Find ∠EBA.
View Solution

