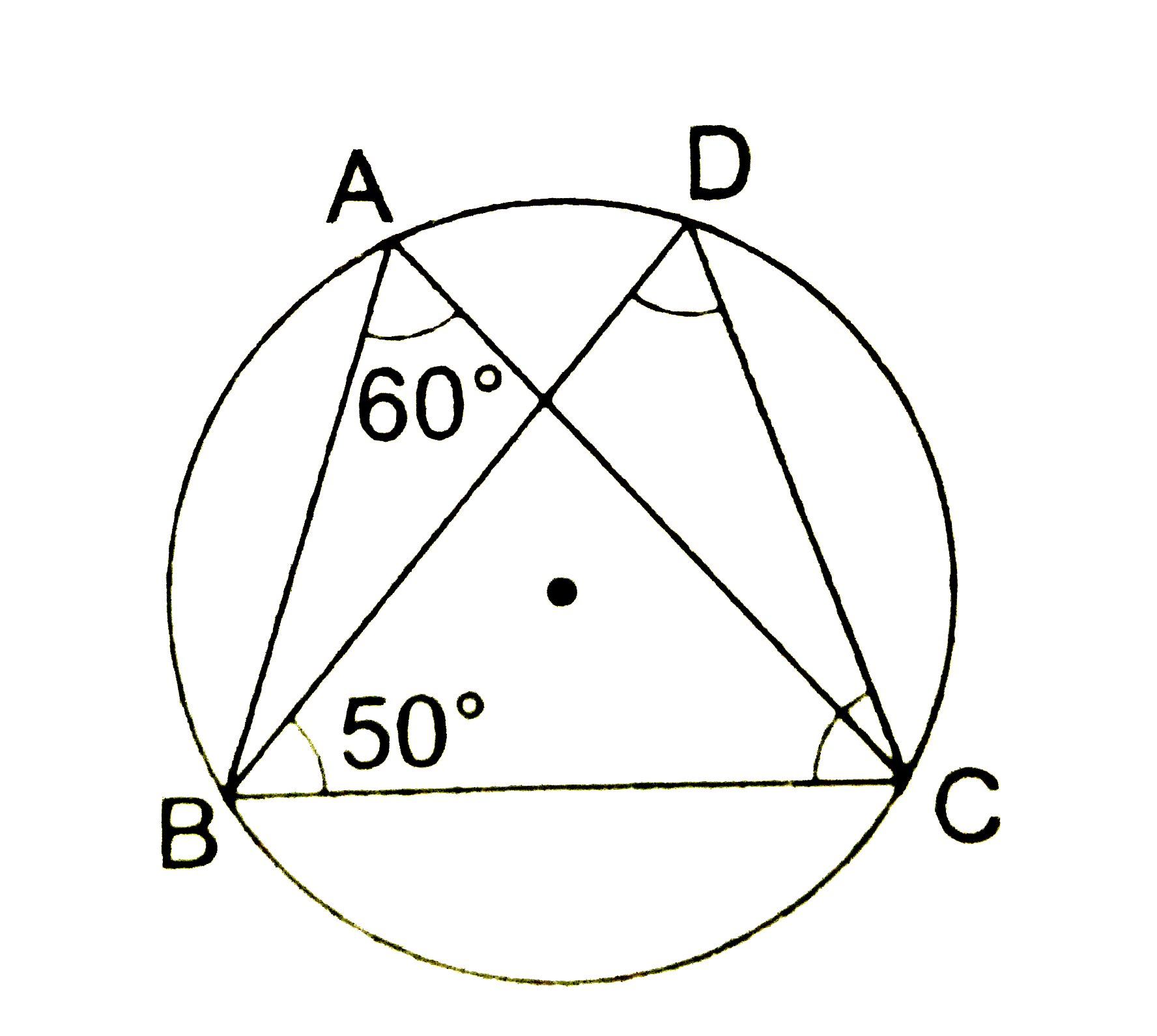
In the given figure, ΔABC and ΔDBC arre inscribed in a circle such that ∠BAC=60∘ and ∠DBC=50∘ . Then , ∠BCD=?
A
50∘
B
60∘
C
70∘
D
80∘
Video Solution
Text Solution
The correct Answer is:C
∠BDC=∠BAC=60∘(∠s in the same segment of a circle ).
In ΔBDC,∠DBC+∠BDC+∠BCD=180∘.
∴50∘+60∘+∠BCD=180∘⇒∠BCD=70∘
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)5videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B16videos
BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, ΔABC is inscribed in a circle and the bisector of ∠A meets BC in D and the circle in E. If ∠ECD=30∘, what is ∠A ?
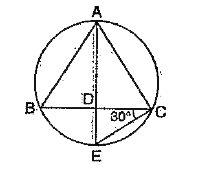 A60∘B45∘C70∘D150∘
A60∘B45∘C70∘D150∘ - Question 2 - Select One
If a right angled triangle ABC of maximum Δ area is inscribed in a circle of radius R , then
AΔ=2R2Br=(√2−1)RC1r1+1r2+1r3=√2−1RDs=(√2−1)R
In the given figure if ∠DBC=70∘ and ∠BAC=40∘ then find the value of ∠BCD
View SolutionIn cyclic quadrilateral ABCD, Diagonals AC and BD intersect at P. If ∠DBC=70∘ and ∠BAC=30∘ then find ∠BCD
View SolutionIn the given figure CDP is a straight line ΔAQD is an equilateral triangle ∠BAR=90∘,∠QAR=135∘,∠BCD=106∘ and ∠ABC=100∘. Then, ∠PDQ equals
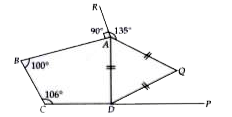 View Solution
View SolutionIn this figure ∠DBC=30∘and∠BCD=110∘. Find ∠BAC
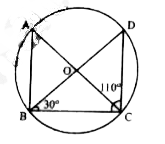 View Solution
View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn ΔABC,AC=BC and ∠BAC=70∘. Find ∠BCA
View Solution


