In the given figure, AOB is a diameter and ABCD is a cyclic quadrilateral. If ∠ADC=120∘ then ∠BAC=?
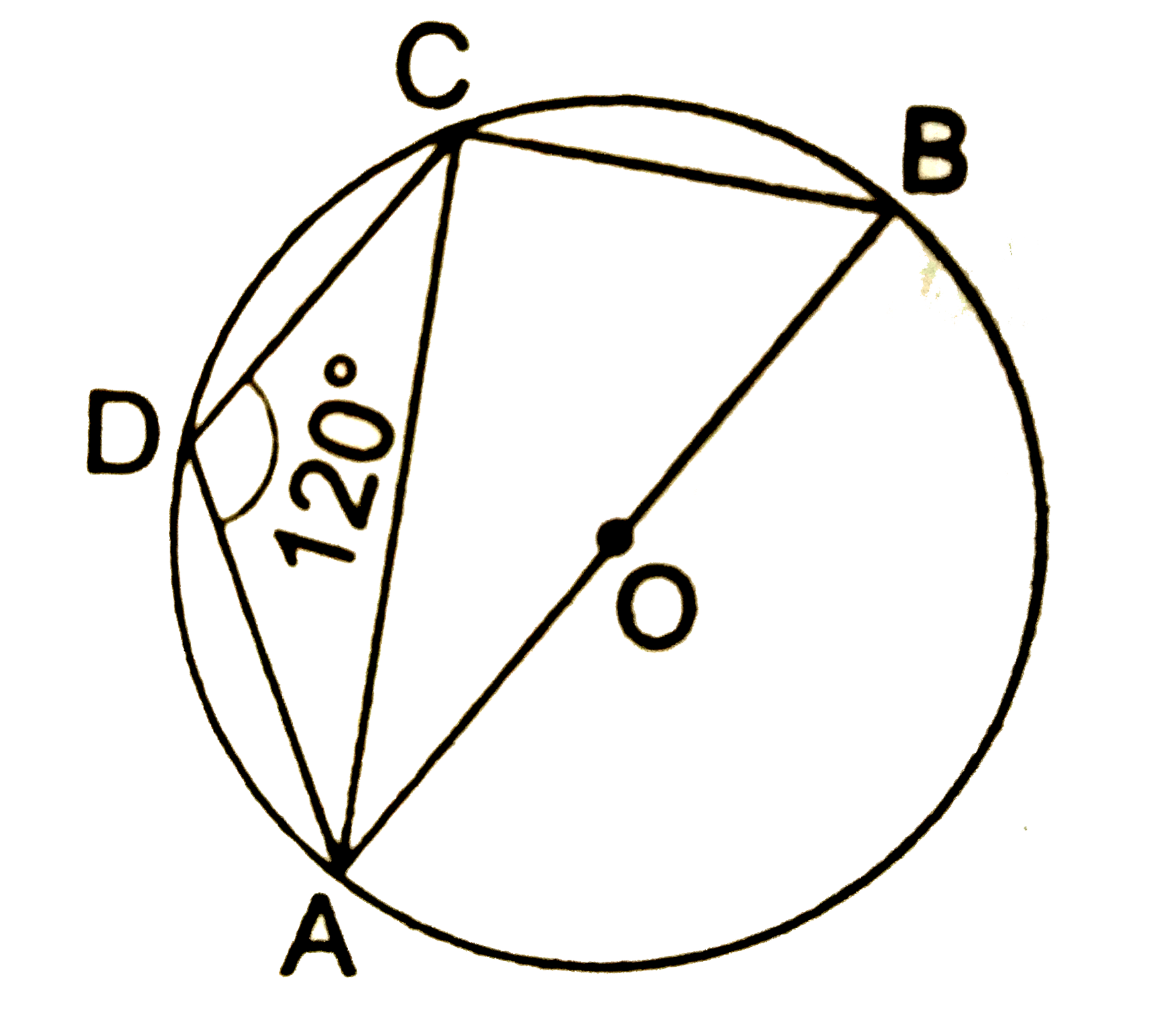
A
60∘
B
30∘
C
20∘
D
45∘
Video Solution
Text Solution
The correct Answer is:B
∠ABC+∠ADC=180∘(opp. ∠s of cyclic quad. )
⇒∠ABC+120∘=180∘⇒∠ABC=60∘
Also, ∠ACB=90∘( angle in a semicircle) .
In ΔACB,∠BAC+∠ACB+∠ABC=180∘
⇒∠BAC+90∘+60∘=180∘⇒∠BAC=30∘
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)5videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B16videos
BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)20videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, ABCD and ABEF aretwo cyclic quadrilaterals. If ∠BCD=110∘ then ∠BEF=?
 A55∘B70∘C90∘D110∘
A55∘B70∘C90∘D110∘ - Question 2 - Select One
In the given figure, ABCD is a cyclic quadrilateral and AB is diameter. ∠ADC=140∘, then find ∠BAC :
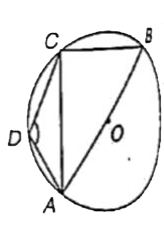 A45∘B40∘C50∘Dnone of the above
A45∘B40∘C50∘Dnone of the above - Question 3 - Select One
In the given figure PAQ is the tangent of the circle at point A and ABCD is a cyclic quadrilateral.
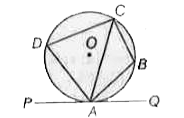
If ∠CAQ=70∘, then ∠ABC isA110∘B70∘C80∘D90∘
In Figure ABCD is a cyclic quadrilateral. If ∠BCD=1000and ∠ABD=700, find ∠ADB
View SolutionThe given figure shows a quadrilateral ABCD.
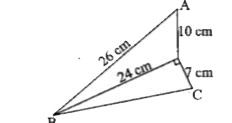
What is the area of quadrilateral ABCD?View SolutionIn the given figure, ABCD is a cyclic quadrilateral; O is the centre of the circle.If ∠BOD=160∘, then find ∠BPD.
View SolutionIn the adjoining figure, if ABCD is a cyclic quadrilateral, find the value of x.
 View Solution
View SolutionABCD is a cyclic quadrilateral and AD is a diameter. If ∠DAC=55∘ then value of ∠ABC is
View Solution

