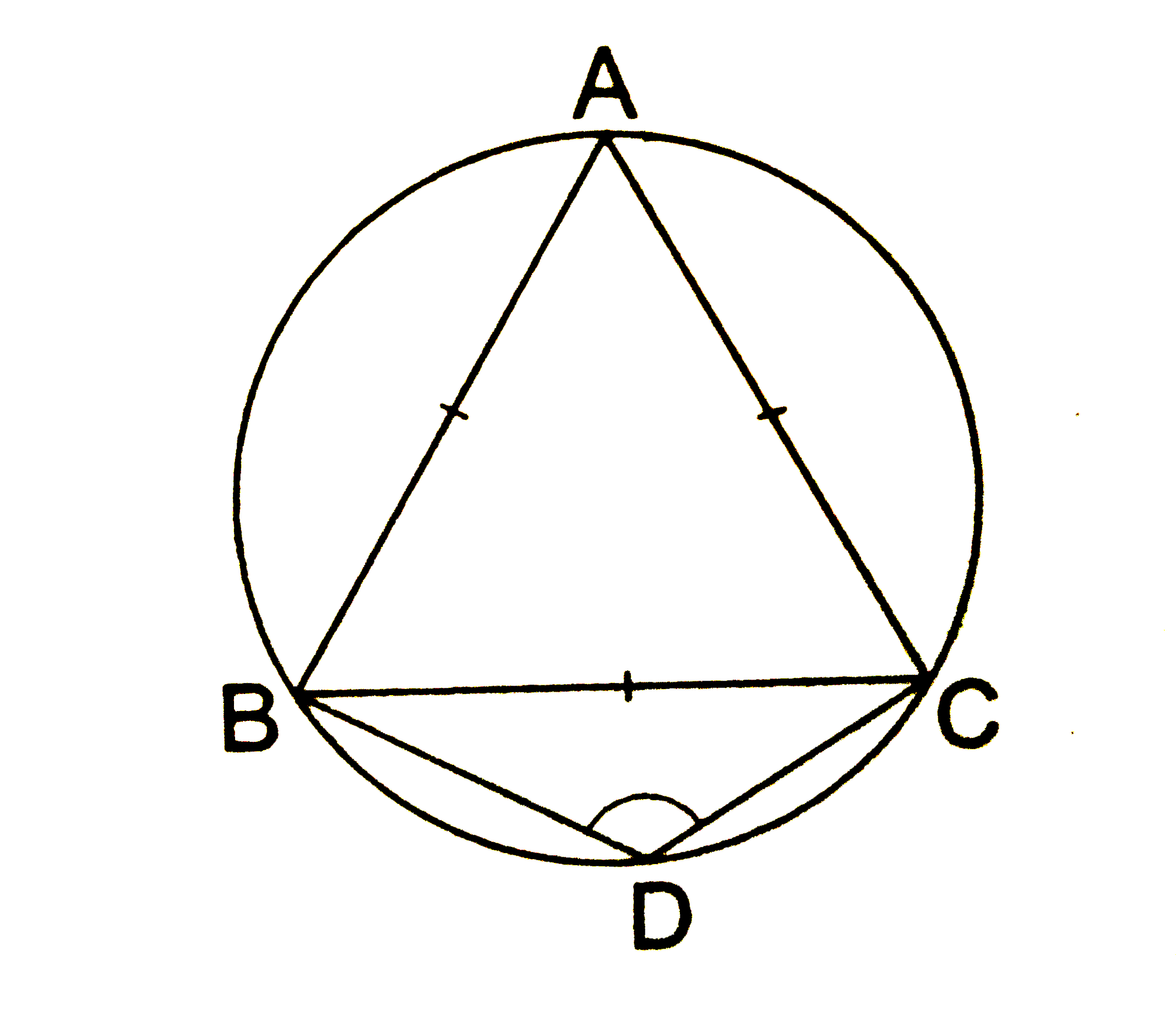
In the given , equilateral $Δ A B C$ is inscribed in a circle and ABDC is a quadrialteral, as shown. Then , $∠ B D C = ?$

A

$90^{\circ}$

B

$60^{\circ}$

C

$120^{\circ}$

D

$150^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Since $Δ A B C$ is an equilateral triangle, each of its angles is $60^{\circ}$
$∴ ∠ B A C = 60^{\circ}$
In cyclic quad. ABDC, we have
$∴ ∠ B A C + ∠ B D C = 180^{\circ} \Rightarrow 60^{\circ} + ∠ B D C = 180^{\circ} \Rightarrow ∠ B D C = 120^{\circ}$

|

Updated on:21/07/2023

Class 9 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Area of an equilateral triangle inscribed in a circle of radius a is
A $\sqrt{3} a^{2} / 4$
B $π a^{2} / 3$
C $3 \sqrt{3} a^{2} / 4$
D $\sqrt{3} π a^{2} / 4$
Question 2 - Select One
An equilateral triangle is inscribed in a circle of radius $6$ cm. Find its side.
A $6 \sqrt{3}$
B $\frac{6}{\sqrt{3}}$
C $8 \sqrt{3}$
D $2 \sqrt{3}$
Question 3 - Select One
Equilateral $Δ$ ABC is inscribed in a circle with centre P. Then, $∠ B P C$ = ..........
A $60^{\circ}$
B $90^{\circ}$
C $120^{\circ}$
D $75^{\circ}$

RS AGGARWAL-CIRCLES -MULTIPLE CHOICE QUESTION(MCQ)

Home
Ask Doubt
Profile