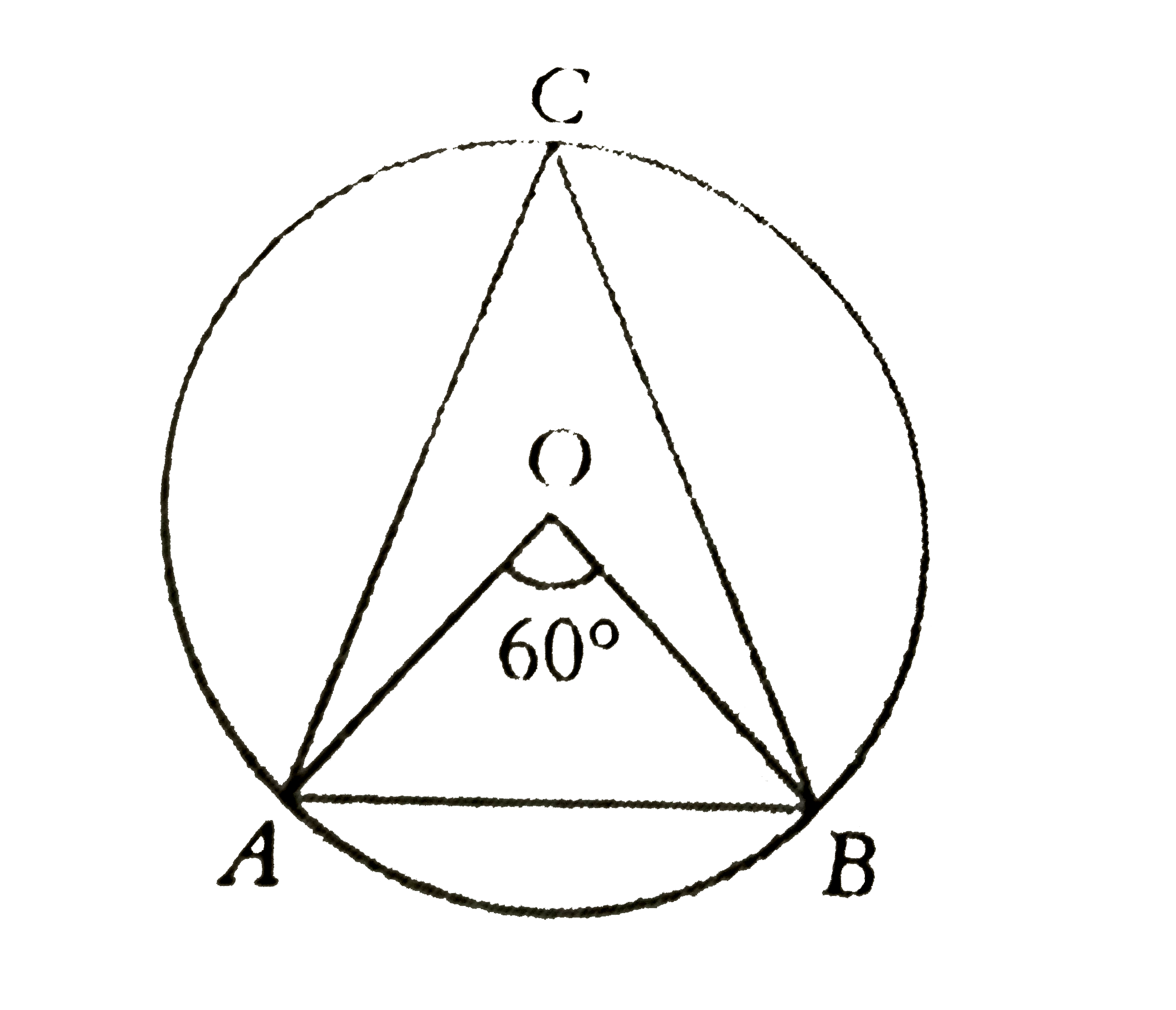
In the given figure, ∠AOB=90∘ and ∠ABC=30∘ . Then ∠CAO=?

A
30∘
B
45∘
C
60∘
D
90∘
Video Solution
Text Solution
The correct Answer is:C
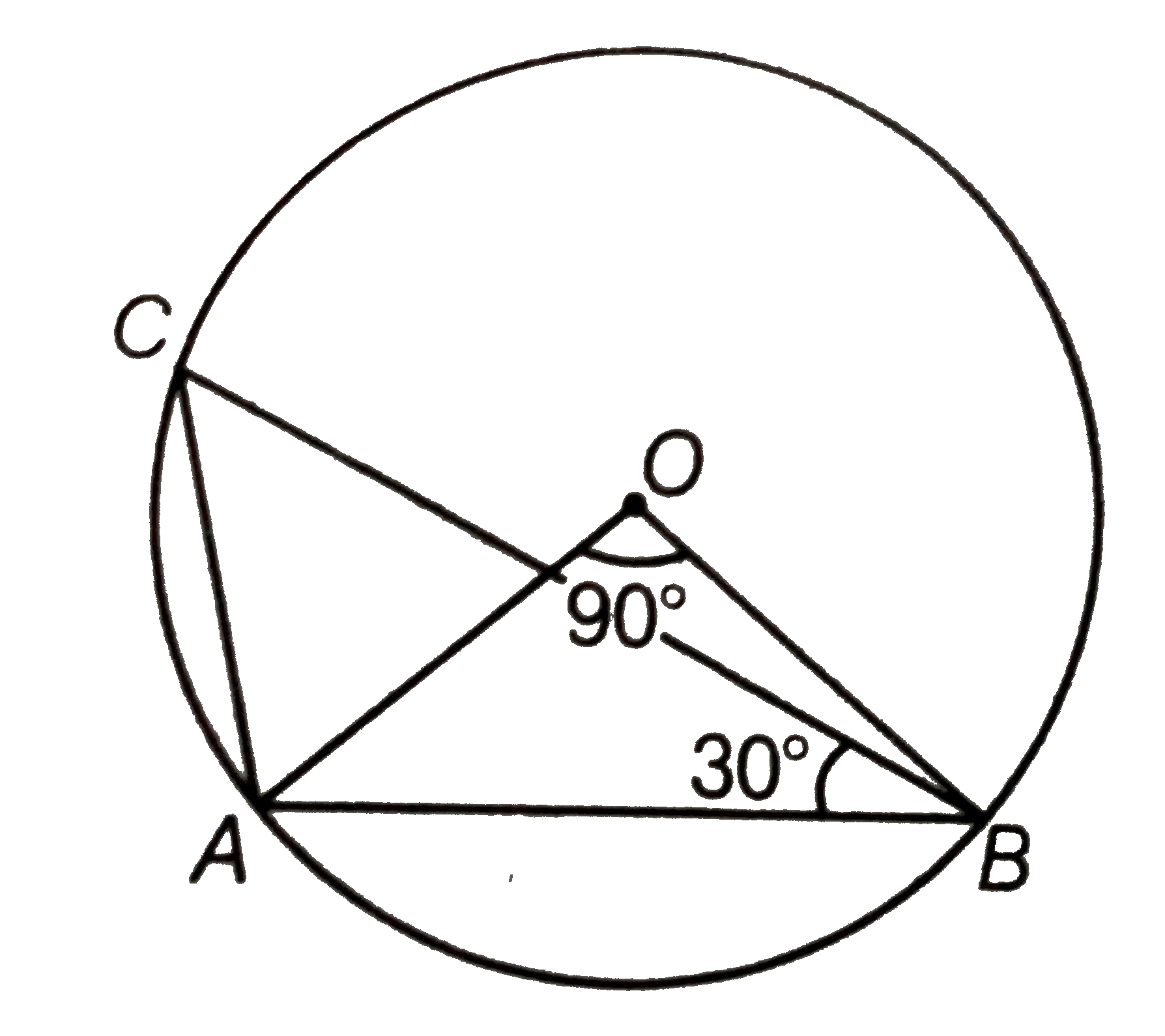
∠AOB=2∠ACB⇒∠ACB=12∠AOB=(12×90∘)=45∘
∠COA=2∠CBA=(2×30∘)=60∘
∴∠COD=180∘−∠COA=180∘−60∘=120∘
⇒∠CAO=12∠COD=12×120∘=60∘
|
Topper's Solved these Questions
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:Multiple Choice Questions (Mcq)
Explore 5 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBook:RS AGGARWALChapter:BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONExercise:EXERCISE 17B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
Similar Questions
Knowledge Check
In the given figure, find ∠AOB.
 A140∘B120∘C150∘D160∘
A140∘B120∘C150∘D160∘In the given figure, AOB is a straight line, ∠AOC = (3x−8)∘, ∠COD = 50∘ and ∠BOD = (x+10)∘. The value of x is
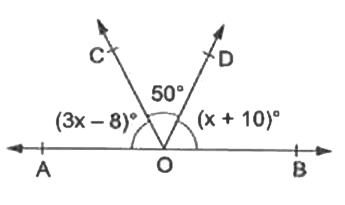 A32B42C36D52
A32B42C36D52In the given figure, AOB is a straight line, ∠AOC = 68∘ and ∠BOC=X∘ The value of x is
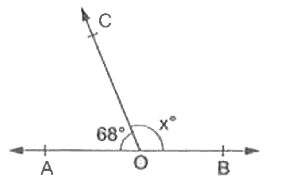 A32B22C112D132
A32B22C112D132
In the given figure, find ∠ABC.

View SolutionIn the given figure DA⊥OP and DB⊥OQand ∠ADB=170∘ find ∠AOB.
View SolutionIn the given figure, , O is the centre of a circle and ∠AOB=140∘. Then , ∠ACB=?

View SolutionIn figure, if ∠AOB=90∘and∠ABC=30∘, then∠CAO is equal to
View SolutionIn the given figure, AOB is a straight line, ∠AOC=56∘ and ∠BOC=x∘. The value of x is
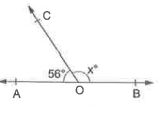
View Solution