M and N divide the side AB of a triangle ABC into three equal parts . Through M and N, lines are drawn parallel to BC and intersecting AC at points P and Q respectively. Prove that P and Q divide AC into three equal parts.
To prove that points P and Q divide line segment AC into three equal parts, we will follow these steps:
Step 1: Understand the given information
We have triangle ABC with points M and N dividing side AB into three equal parts. This means:
- AM = MN = NB
Step 2: Draw lines parallel to BC
Draw lines through points M and N that are parallel to side BC. Let these lines intersect AC at points P and Q respectively.
Step 3: Establish relationships using the midpoint theorem
Since M is the midpoint of AN (because AM = MN), we can apply the midpoint theorem. According to the midpoint theorem:
- If a line segment is drawn from a midpoint of one side of a triangle to the opposite side and is parallel to the other side, then it divides the other side into two equal parts.
Step 4: Apply the midpoint theorem in triangle ANQ
In triangle ANQ:
- M is the midpoint of AN.
- Line MP is parallel to line QN (since both are drawn parallel to BC).
Thus, by the midpoint theorem, P is the midpoint of AQ.
Step 5: Establish the first equality
From the above, we have:
- AP = PQ (let this be Equation 1).
Step 6: Analyze triangle BCM
Now consider triangle BCM. Since N is the midpoint of MB (because MN = NB), we can again apply the midpoint theorem:
- Line NR is parallel to BC.
Thus, R is the midpoint of CM.
Step 7: Apply the midpoint theorem in triangle CPM
In triangle CPM:
- R is the midpoint of CM.
- Line QR is parallel to line PM (since both are drawn parallel to BC).
Thus, by the midpoint theorem, Q is the midpoint of CP.
Step 8: Establish the second equality
From the above, we have:
- PQ = QC (let this be Equation 2).
Step 9: Combine the results
From Equations 1 and 2, we have:
- AP = PQ and PQ = QC.
Thus, we can conclude:
- AP = PQ = QC.
Step 10: Conclusion
Therefore, points P and Q divide line segment AC into three equal parts, which is what we needed to prove.
---
We have triangle ABC with points M and N dividing side AB into three equal parts. This means:
- AM = MN = NB
Draw lines through points M and N that are parallel to side BC. Let these lines intersect AC at points P and Q respectively.
Since M is the midpoint of AN (because AM = MN), we can apply the midpoint theorem. According to the midpoint theorem:
- If a line segment is drawn from a midpoint of one side of a triangle to the opposite side and is parallel to the other side, then it divides the other side into two equal parts.
In triangle ANQ:
- M is the midpoint of AN.
- Line MP is parallel to line QN (since both are drawn parallel to BC).
Thus, by the midpoint theorem, P is the midpoint of AQ.
From the above, we have:
- AP = PQ (let this be Equation 1).
Now consider triangle BCM. Since N is the midpoint of MB (because MN = NB), we can again apply the midpoint theorem:
- Line NR is parallel to BC.
Thus, R is the midpoint of CM.
In triangle CPM:
- R is the midpoint of CM.
- Line QR is parallel to line PM (since both are drawn parallel to BC).
Thus, by the midpoint theorem, Q is the midpoint of CP.
From the above, we have:
- PQ = QC (let this be Equation 2).
From Equations 1 and 2, we have:
- AP = PQ and PQ = QC.
- AP = PQ = QC.
Therefore, points P and Q divide line segment AC into three equal parts, which is what we needed to prove.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - PYTHAGORAS THEOREM
5 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - RECTILINEAR FIGURES
6 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - INEQUALITIES
7 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
ABC is a triangle A line is drawn parallel to BC to meet AB and AC in D and E respectively. Prove that the median through A bisects DE.
View SolutionIn triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and Glines are drawn parallel to AB which meet side BC at points M and N respectively.
Prove that : BM = MN = NC.
View SolutionPQR is a triangle in which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT.
View SolutionPQR is a triangle is which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT
View SolutionBC is an equilateral triangle. A circle is drawn with centre A so that it cuts AB and AC at points M and N respectively. Prove that BN = CM
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
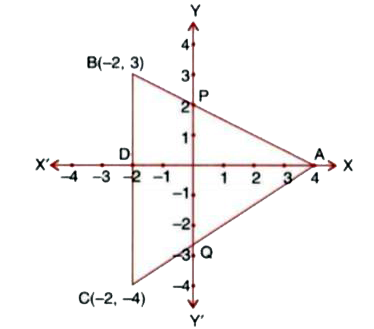
Find the ratio in which divides AC.
View SolutionIn the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.

(iii) Find the ratio in which Q divides AC.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Find AB, if EF=4.8cm.
View Solution