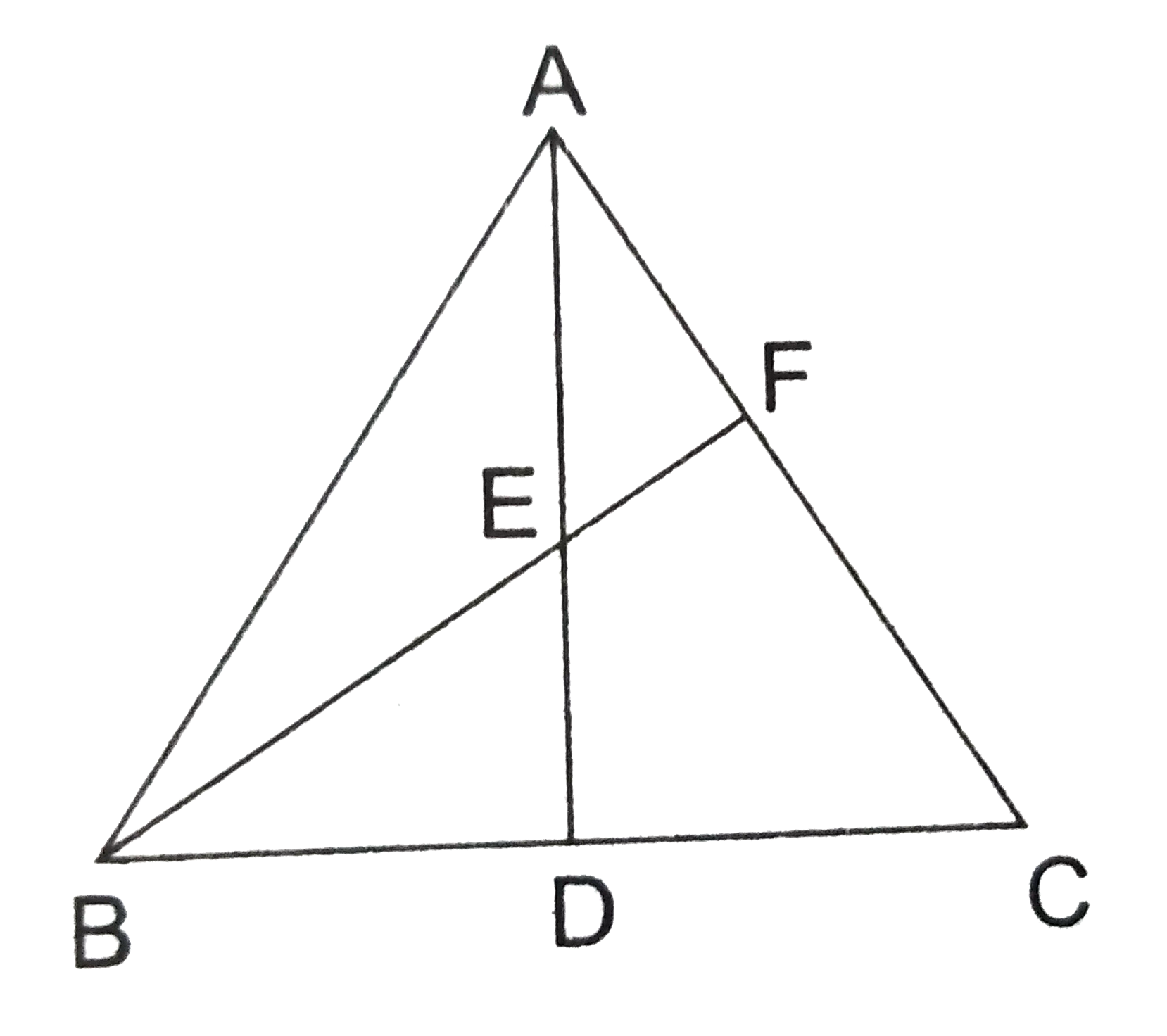
In the given figure, AD is a median of △ABC and E is the midpoint of AD. If BE is joined and produced to meet AC in F then AF = ?
A
12AC
B
13AC
C
23AC
D
34AC
Video Solution
Text Solution
The correct Answer is:B
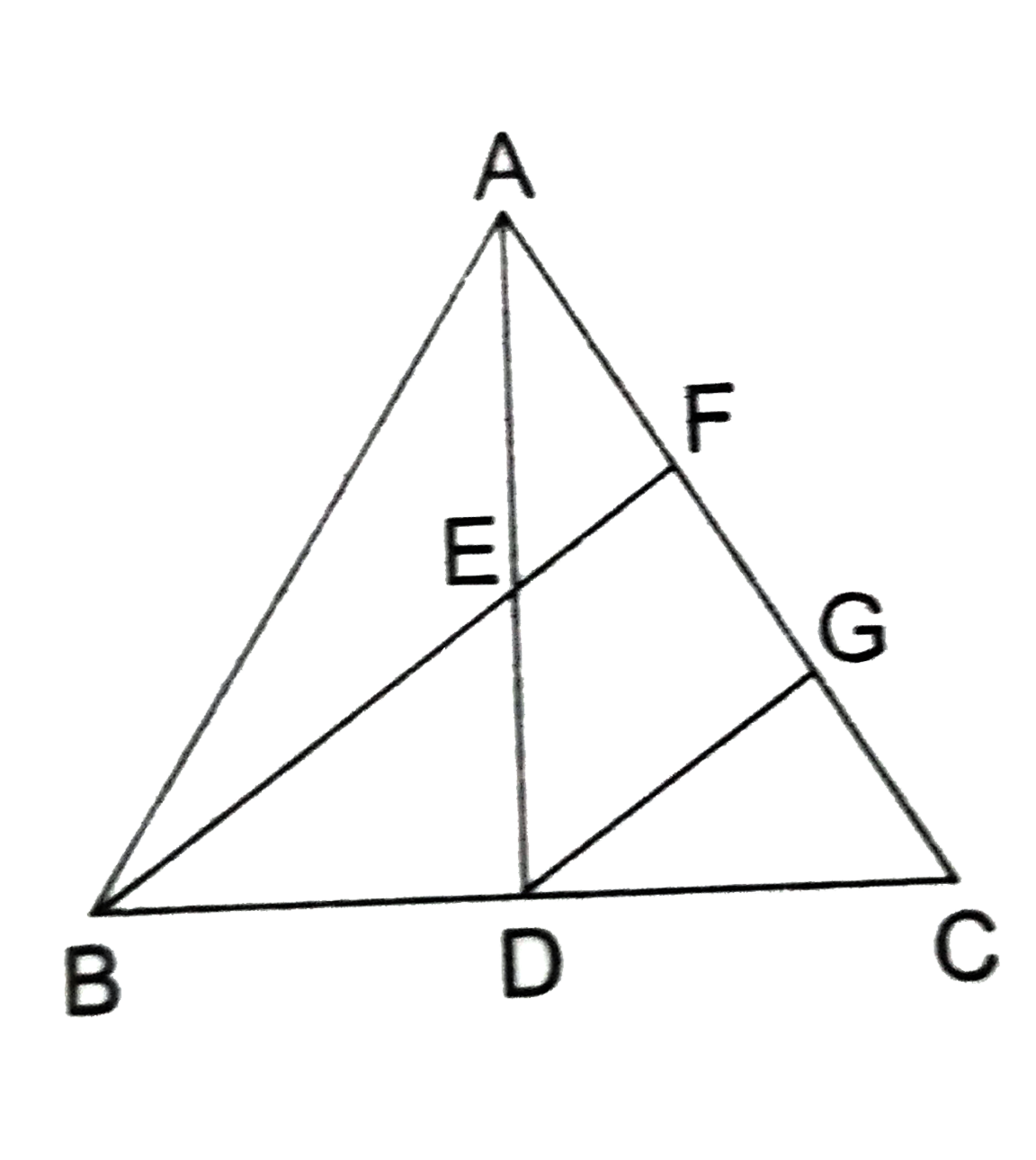
Let G be the midpoint of FC. Join DG.
In △BCF,D is the midpoint of BC and G is the midpoint of FC.
∴DG||BF⇒DG||EF.
In △ADG,E is the midpoint of AD and EF||DG.
So, F is the midpoint of AG.
∴AF=FG=GC [∵ G is the midpoint of FC].
∴AF=13AC.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Short-Answer Questions1videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Assertion - and - Reason Type MCQ4videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)47videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
E is a mid-point of median AD of ΔABC. BE is extended to meet AC at F. In what ratio AC is divided by F.
A2:3B2:1C1:3D3:2 - Question 2 - Select One
If in a △ABC,A=π3andAD is the median, then
A2AD2=b2+c2+bcB4AD2=b2+c2+bcC6AD2=b2+c2+bcDnone of these - Question 3 - Select One
In the given figure AD=BC,AC=BD. Then ΔPAB is
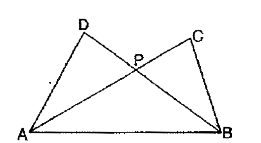 AequilateralBright angledCscaleneDisosceles
AequilateralBright angledCscaleneDisosceles
In a triangle ABC, AD is the median through A and E is the midpoint of AD, and BE produced meets AC at F. Then AF is equal to
View SolutionIn ABC,AD is the median through A and E is the mid-point of AD . BE produced meets AC in F (Figure). Prove that AF=13AC.
View SolutionIn ΔABC,D is the mid-pointpoint of BC and E is mid-point of AD.BE is produced to meet the side AC in F.Then BF is equal to
View SolutionIn the given figure of AD = CB then prove that AC = BD
 View Solution
View SolutionIn Figure, AD is the median and DEAB. Prove that BE is the median.
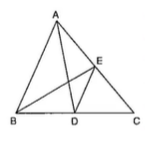 View Solution
View Solution


