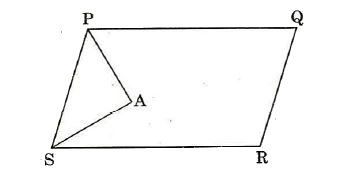
In the given figure, ABCD is a parallelogram, M is the midpoint of BD and BD bisects ∠B as well as ∠D. Then, ∠AMB=?

A
45∘
B
60∘
C
90∘
D
30∘
Video Solution
Text Solution
The correct Answer is:C
∠B=∠D⇒12∠B=12∠D⇒∠ADB=∠ABD.
∴△ABD is isosoceles and M is the midpoint of BD.
∴AM⊥BD and hence ∠AMB=90∘.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Short-Answer Questions1videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Assertion - and - Reason Type MCQ4videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)47videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
In a parallelogram ABCD, M is the midpoint of BD and BM is bisector of ∠B. The measure of ∠AMB is.
A45∘B60∘C90∘D120∘ - Question 2 - Select One
If ABCD is a parallelogram, then −−→AC−−−→BD=
A4−−→ABB3−−→ABC2−−→ABD−−→AB - Question 3 - Select One
In the given figure, ABCD is a parallelogram in which ∠BAD=75∘and∠CBD=60∘. Then, ∠BDC is equal to
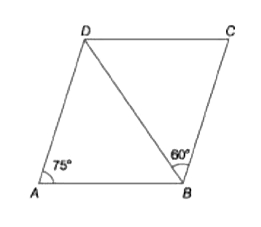 A60∘B75∘C45∘D50∘
A60∘B75∘C45∘D50∘
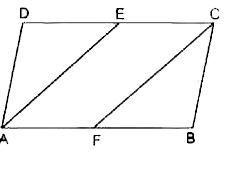
In the adjacent figure , ABCD is a parallelogram and line segments AE and CF bisect the angles A and C respectively . Show that AE∣∣CF.
 View Solution
View SolutionIn the given figure, AD is bisector of angle ∠CAB and BD is bisector of ∠CBF. If the angle at C is 34∘, the angle ∠ADB is:
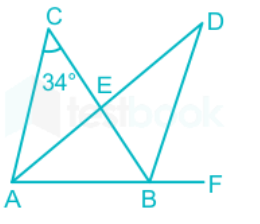 View Solution
View SolutionIn quadrilateral ABCD, BA = BC and DA = DC. Prove that BD bisects ∠ ABC as well as ∠ ADC.
View SolutionThe diagonal BD of a quadrilateral ABCD bisects ∠Band∠D, then :
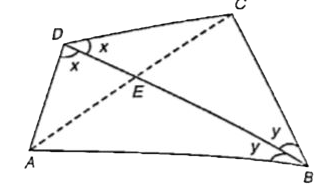 View Solution
View SolutionABCD is a parallelogram with AC and BD as diagonals. Then, A→C−B→D=
View Solution