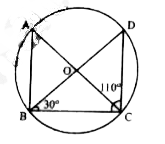
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O such that $∠ D A C = 30^{\circ} and ∠ A O B = 70^{\circ}, Then, ∠ D B C =$ ?

A

$40^{\circ}$

B

$35^{\circ}$

C

$45^{\circ}$

D

$50^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$∠ A O C = ∠ D A C = 30^{\circ} (alt. interior ∠)$
$\Rightarrow ∠ O C B = 30^{\circ}$ .
$∠ A O B + ∠ B O C = 180^{\circ} \Rightarrow 70^{\circ} + ∠ B O C = 180^{\circ} \Rightarrow ∠ B O C = 110^{\circ} .$
In $△ O B C, ∠ B O C + ∠ O C B + ∠ O B C = 180^{\circ}$
$\Rightarrow 110^{\circ} + 30^{\circ} + ∠ O B C = 180^{\circ} \Rightarrow ∠ O B C = 40^{\circ} .$

|

Updated on:21/07/2023

Class 9 MATHS QUADRILATERALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The diagonals $A C$ and $B D$ of a parallelogram $A B C D$ intersect each other at the point O. If $∠ D A C = 32^{\circ} and ∠ A O B = 70^{\circ}, find ∠ D B C .$
A $35^{\circ}$
B $38^{\circ}$
C $40^{\circ}$
D $45^{\circ}$
Question 2 - Select One
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If $∠ D A C = 32^{\circ} and ∠ A O B = 70^{\circ}$ , then $∠ D B C$ is equal to
A $24^{\circ}$
B $86^{\circ}$
C $38^{\circ}$
D $32^{\circ}$
Question 3 - Select One
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If $∠ D A C = 32^{\circ} and ∠ A O B = 70^{\circ}, then ∠ D B C$ is equal to
A $24^{\circ}$
B $86^{\circ}$
C $38^{\circ}$
D $32^{\circ}$

RS AGGARWAL-QUADRILATERALS-MULTIPLE-CHOICE QUESTIONS (MCQ)

Home
Ask Doubt
Profile