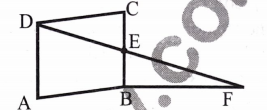
In the given figure, ABCD is a ||gm and E is the mid-point of BC. Also, DE and AB when produced meet at F. Then.
AF=32AB
AF=2AB
AF=3AB
AF2=2AB2
The correct Answer is:B
In ∠EDCand∠EFB, we have
∠DCE=∠EBF (alt. interior ∠),
∠DEC=∠FEB (vert. opp. ∠)
andEC=EB.
∴△EDC≅△EFB and therefore, BF=DC.
∴AF=(AB+BF)=(AB+DC)=2AB.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Short-Answer Questions1videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Assertion - and - Reason Type MCQ4videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)47videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
Similar Questions
In the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.
 View Solution
View SolutionIn the given figure, ABCD is a parallelogram, in which is the mid-point of ADandO is a point on AC such that AO=14AC. When EO produced, meets AB at F. Prove that F is the mid-point of AB.
View Solution
Knowledge Check
- Question 1 - Select One
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AAN=√3ABBAN=2ABCAN2=32AB2DAN2=2AB2 - Question 2 - Select One
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AA)AN=√3ABBB)AN=2ABCC)AN2=32AB2DD)AN2=2AB2
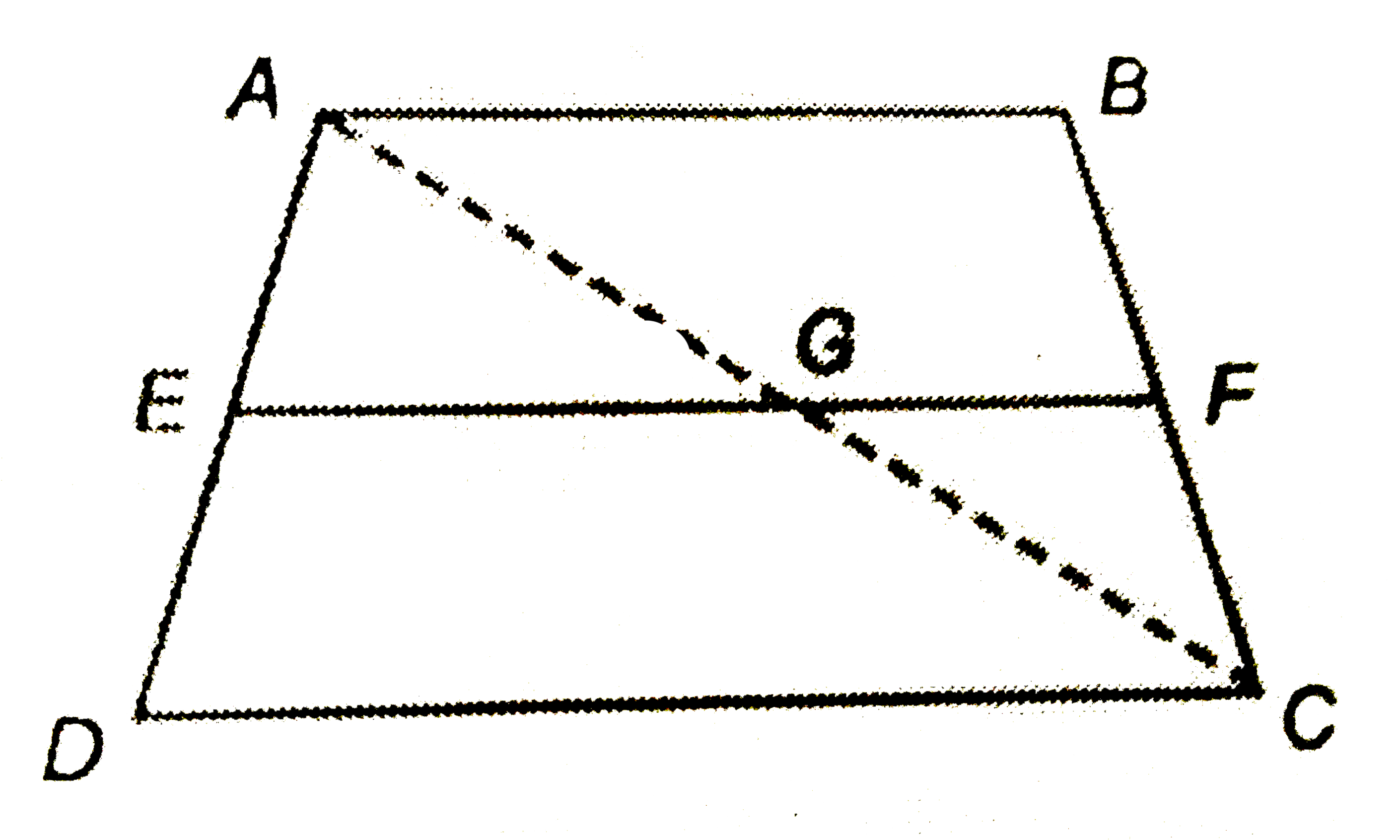
In the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that EF=12(AB+DC).
 View Solution
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
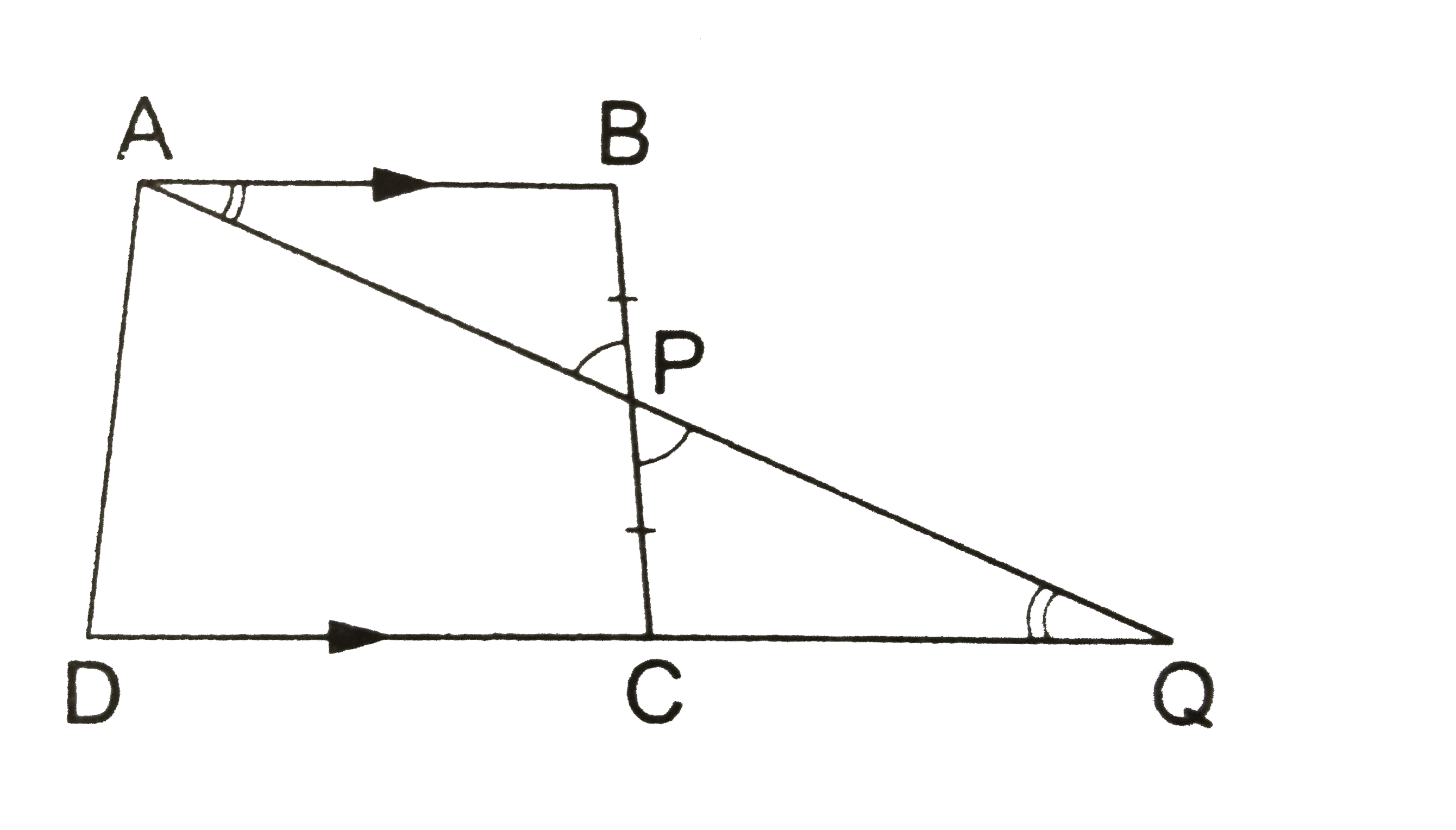
View SolutionIn the given figure ABCD is a quadrilateral in which AB||DC and P is the midpoint of BC. On producing, AP and DC meet at Q. Prove that (i)AB=CQ,(ii)DQ=DC+AB.
 View Solution
View SolutionIn the given figure, ABCD is a rectangle; EandF are the mid-points of the sides BCandCD respectively. What is the ratio of the area of ΔAEF and that of ΔECF?
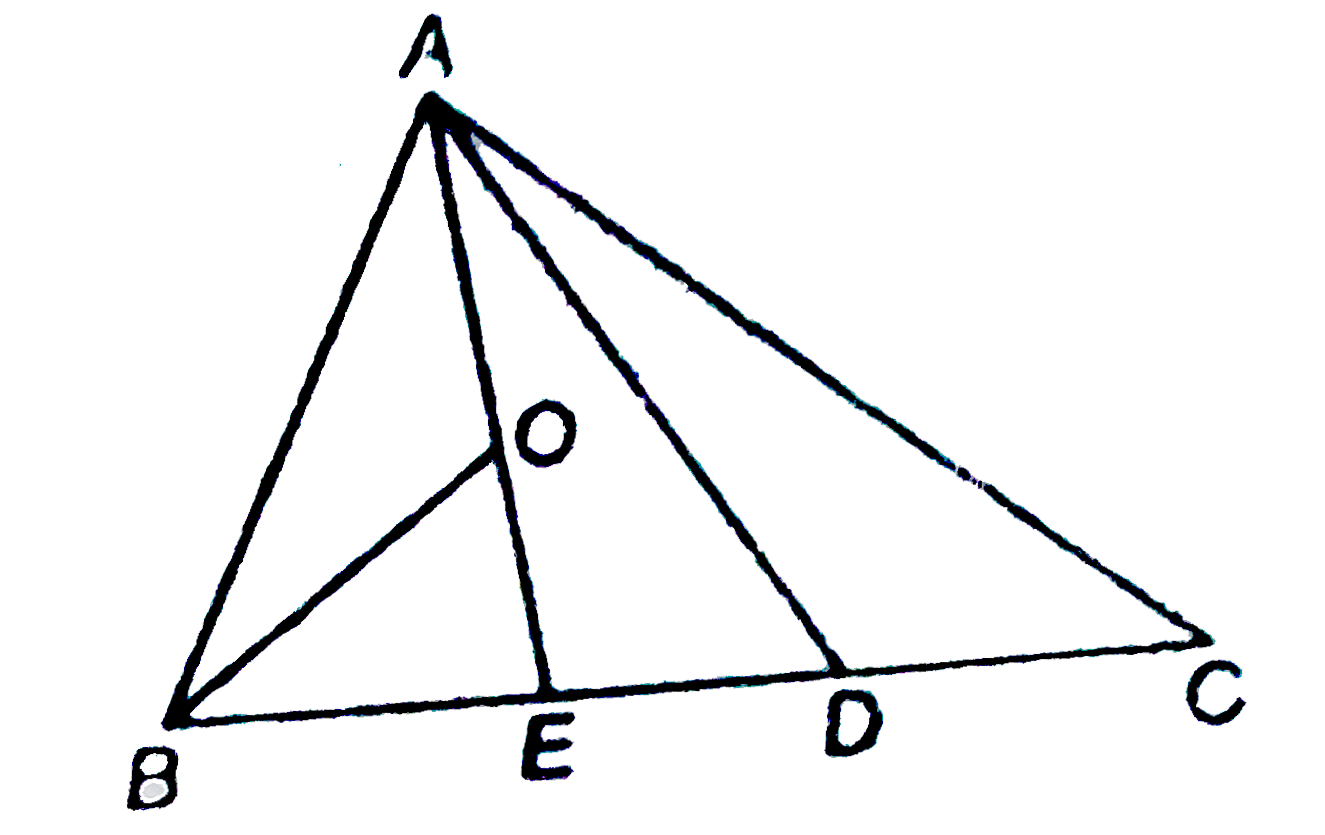
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC
 View Solution
View SolutionIn the given figure, ABCD is a quadrilateral in which AB∣∣DC and P is the midpoint of BC. On producing, AP and DC meet at Q. Prove that (i) AB=CQ, (ii) DQ=DC+AB
View Solution

