The side BC,CA and AB of ΔABC have been produced to D,E and F respectively. ∠BAE+∠CBF+∠ACD=?
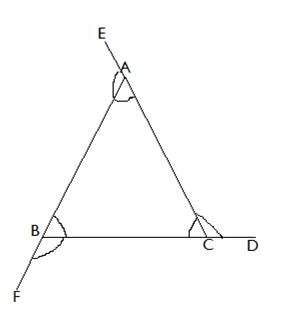
240∘
300∘
320∘
360∘
The correct Answer is:D
Step by step video & image solution for The side BC, CA and AB of DeltaABC have been produced to D, E and F respectively. angleBAE+angleCBF+angleACD=? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Multiple Choice Questions (Mcq)2videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)73videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
In the above figure ( not to scale ) the sides BA,BC and CA ofΔABC are produced to D,F, and E respectively such that ∠ACF=120∘ and ∠BAE=150∘. Then ∠ABC=_____.View SolutionAn exterior angle of a triangle is 1100, and one of the interior opposite angles is 300. Find the other two angles of the triangle.
View Solution
Knowledge Check
- Question 1 - Select One
The sides BC,CA and AB of △ABC have been produced to D, E and F respectively as shown in the figure, forming exterior angles ∠ACD,∠BAEand∠CBF. Then, ∠ACD+∠BAE+∠CBF is equal to
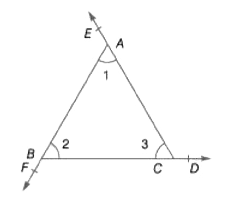A240∘B300∘C320∘D360∘ - Question 2 - Select One
ΔABC is an isosceles triangle and AB = AC. If all the sides AB. BC and CA of a ΔABC touch a circle at D, E and F respectively. Then BE is equal to :
A12 BCB13 BCC14 BCD23 BC - Question 3 - Select One
A circle touches the side BC of ΔABC at D and AB and aC are produced to E and F, respectively. If AB=10cm, AC=8.6 cm and BC=6.4 cm then BE=?
A3.5cmB3.2cmC2.5cmD2.2cm
In the given figure, the sides AB and AC of ΔABC have been extended to D and E respectively. If x>y, show that AB>AC.
View Solution-
In the above figure ( not to scale ) the sides BA,BC and CA ofΔABC are produced to D,F, and E respectively such that ∠ACF=120∘ and ∠BAE=150∘. Then ∠ABC=_____.View Solution In the figure sides AB,BC,CA of ΔABC are produced upto points R,P,F respectively such that AB=BR,BC=CP and CA=AF. Prove that:
(ΔPFR)=7A(ΔABC)
View SolutionThe sides AB, BC and AC of a ΔABC are 12 cm, 8 cm and 10 cm respectively. A circle is inscribed in the triangle touching AB, BC and AC at D, E and F, respectively. The difference between the lengths of AD and CE is:
View SolutionIf D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
View Solution