In the given figure, EAD⊥BCD. Ray FAC cuts ray EAD at a point A such that ∠EAF=30∘ . Also, in ΔBAC,∠BAC=x∘and∠ABC=(x+10)∘. Then the value of x is

20
25
30
35
The correct Answer is:B
∠CAD=∠EAF=30∘ [vert. opp∠s]
∠ACD=180∘−(30∘+90∘)=60∘⇒x+(x+10)=60⇒x=25.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Multiple Choice Questions (Mcq)2videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)73videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
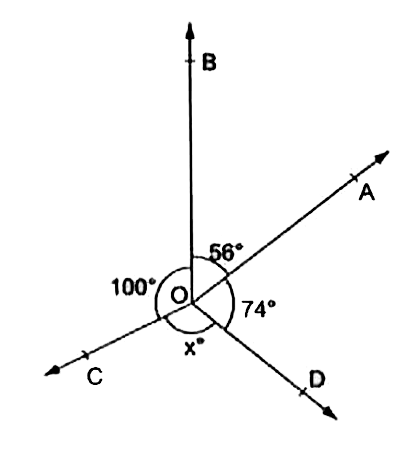
In the given figure, rays OA, OB, OC and OD are such that ∠AOB = 50∘ , ∠BOC = 90∘, ∠COD=70∘ and ∠AOD=x∘. Then, the value of x is
 A50∘B70∘C150∘D90∘
A50∘B70∘C150∘D90∘
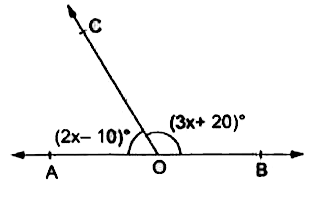
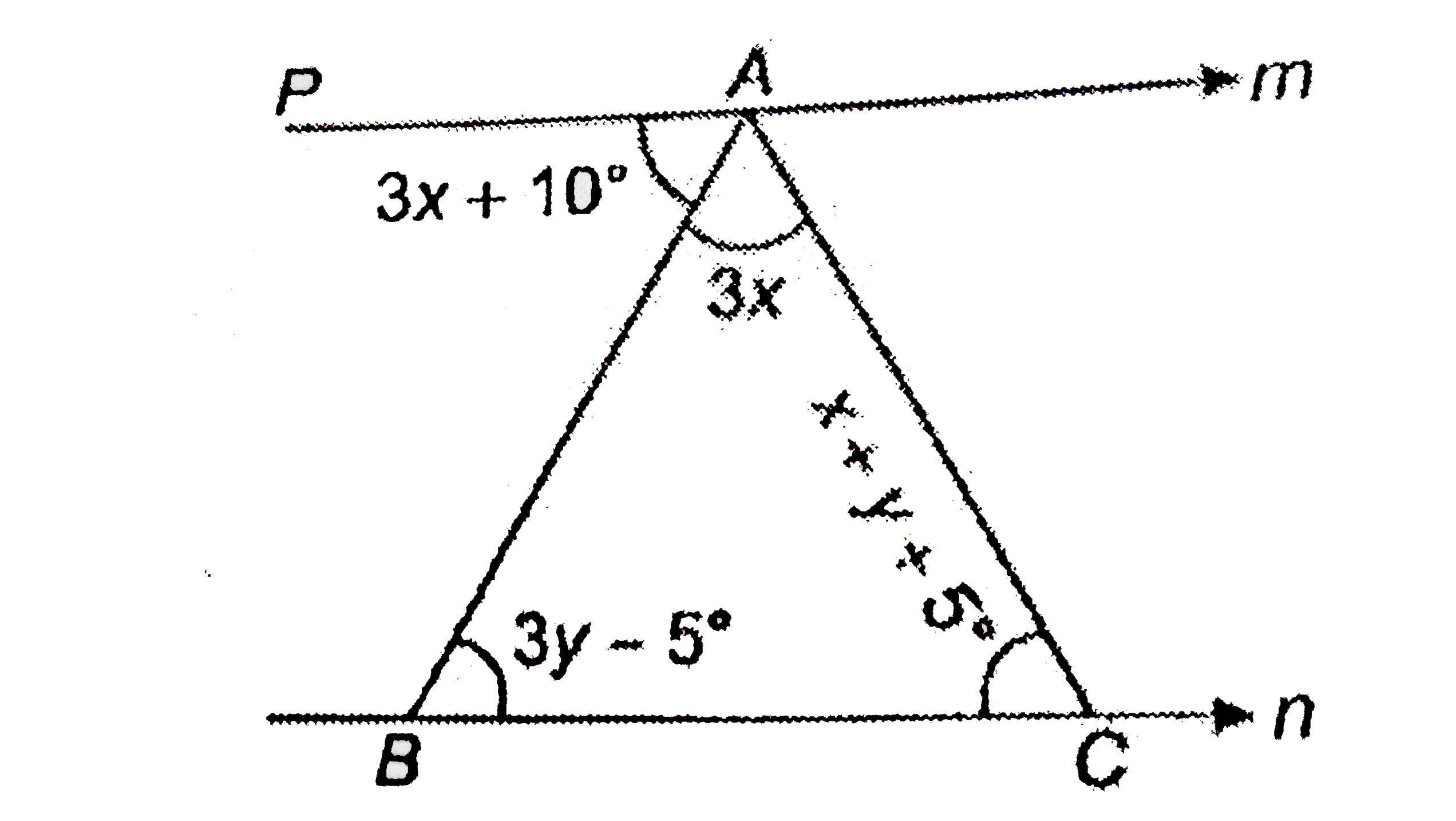
In the given figure, line m is parallel to n. Given that
∠BAP=3x+10∘,∠BAC=3x
∠ABC=3y−5∘,∠ACB=x+y+5∘
Find the valuses of x and y
 View Solution
View SolutionIn the figure.AOB is a straight line and rays OC and OD stand on it.
∠AOC=65∘,∠BOD=70∘and∠COD=x∘,find the value of x. View Solution
View SolutionIn the given figure .AOB is straight a straight line and the ray OC stands on it.If ∠AOC=64∘and∠BOC=x∘,Find the value of x.
View SolutionIn the given figure, AOB is a straight line and OC is a ray such that ∠AOC=(3x+20)∘ and ∠BOC=(2x−10)∘. Find the value of x and hence find (i) ∠AOC
(ii)∠BOC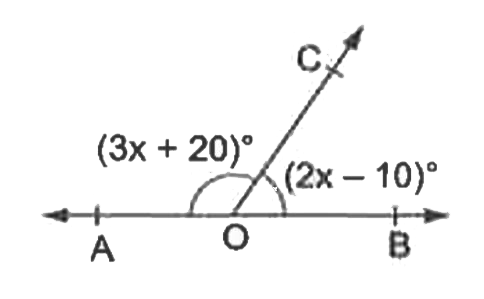 View Solution
View Solution
In the given figure, ray PT is the bisector of ∠QPR.
Find the value of x.
 View Solution
View SolutionIn the given figure, two mirrors X and Y are situated at an angle of 60∘ with each other and a ray of light is incident on mirror X at an angle of 50∘. When the ray is reflected by the mirror Y, then what is angle of reflection at this mirror?
 View Solution
View SolutionIf OB & OA are opposite rays , in the figure then the value of x+y is ____
 View Solution
View Solution