In the given figure, two rays BD and CE intersect at a point A. The side BC of ΔABC have been produced on both sides to points F and G respectively. If ∠ABF=x∘,∠ACG=y∘and∠DAE=z∘ then z=?
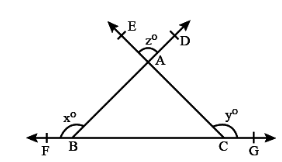
x+y−180
x+y+180
180−(x+y)
x+y+360∘
The correct Answer is:A
∠BAC=∠EAD=z∘,∠ABC=(180∘−x∘),∠BCA=(180∘−y∘),
∠BAC+∠ABC+∠BCA=180∘
⇒z+(180−x)+(180−y)=180⇒z=(x+y)−180∘.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Multiple Choice Questions (Mcq)2videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Multiple Choice Questions (Mcq)73videos
VOLUME AND SURFACE AREA OF SOLIDS
Similar Questions
In the given figure, lines AB and CD intersect at a point O. The sides CA and OB have been produced to E and F respectively such that ∠OAE=x∘and∠DBF=y∘
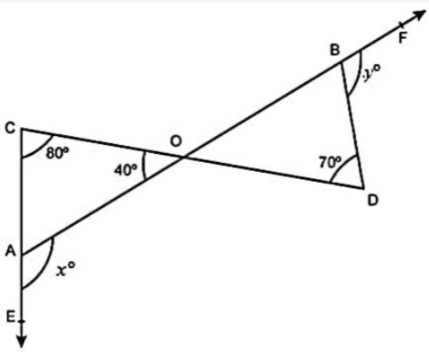
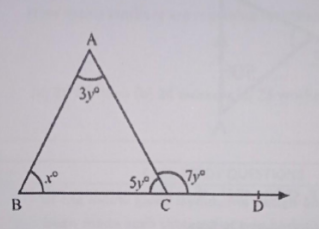
If ∠OCA=80∘,∠COA=40∘and∠BDO=70∘ then x∘+y∘=?View SolutionSide BC of ΔABC has been produced to a point D. If ∠A=3y∘,∠B=x∘,∠C=5y∘and∠ACD=7y∘. Then, the value of x is
 View Solution
View SolutionIn the given figure, the two lines AB and CD intersect at a point O such that ∠BOC=125∘. Find the values of x, y, and z.
View SolutionIn the given figure, the sides AB and AC of ΔABC have been extended to D and E respectively. If x>y, show that AB>AC.
 View Solution
View SolutionAn exterior angle of a triangle is 1100, and one of the interior opposite angles is 300. Find the other two angles of the triangle.
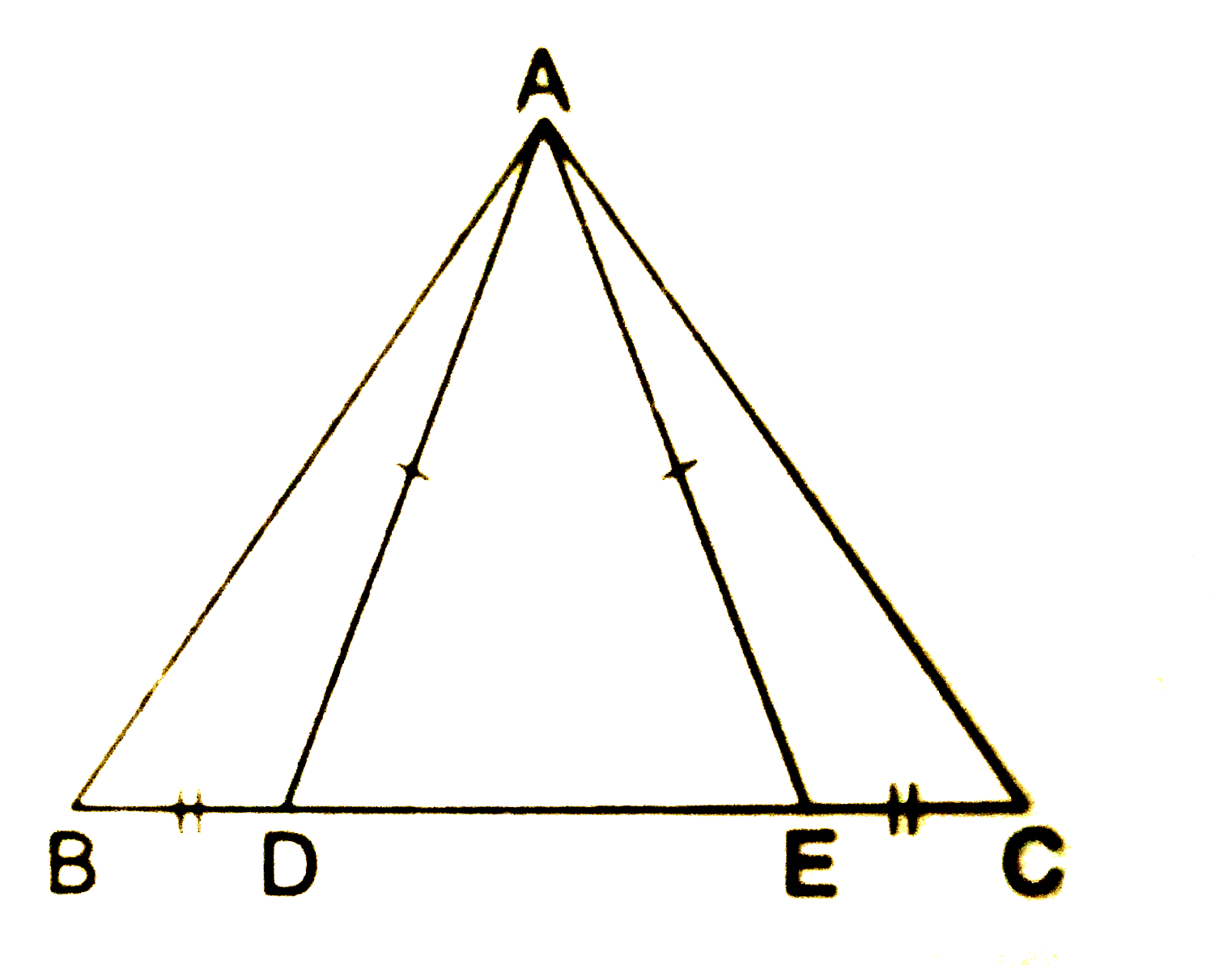
View SolutionIn the given figure, D and E are points on the side BC of a ΔABC such that BD = CE and AD = AE. Show that ΔABD≅ΔACE.
 View Solution
View Solution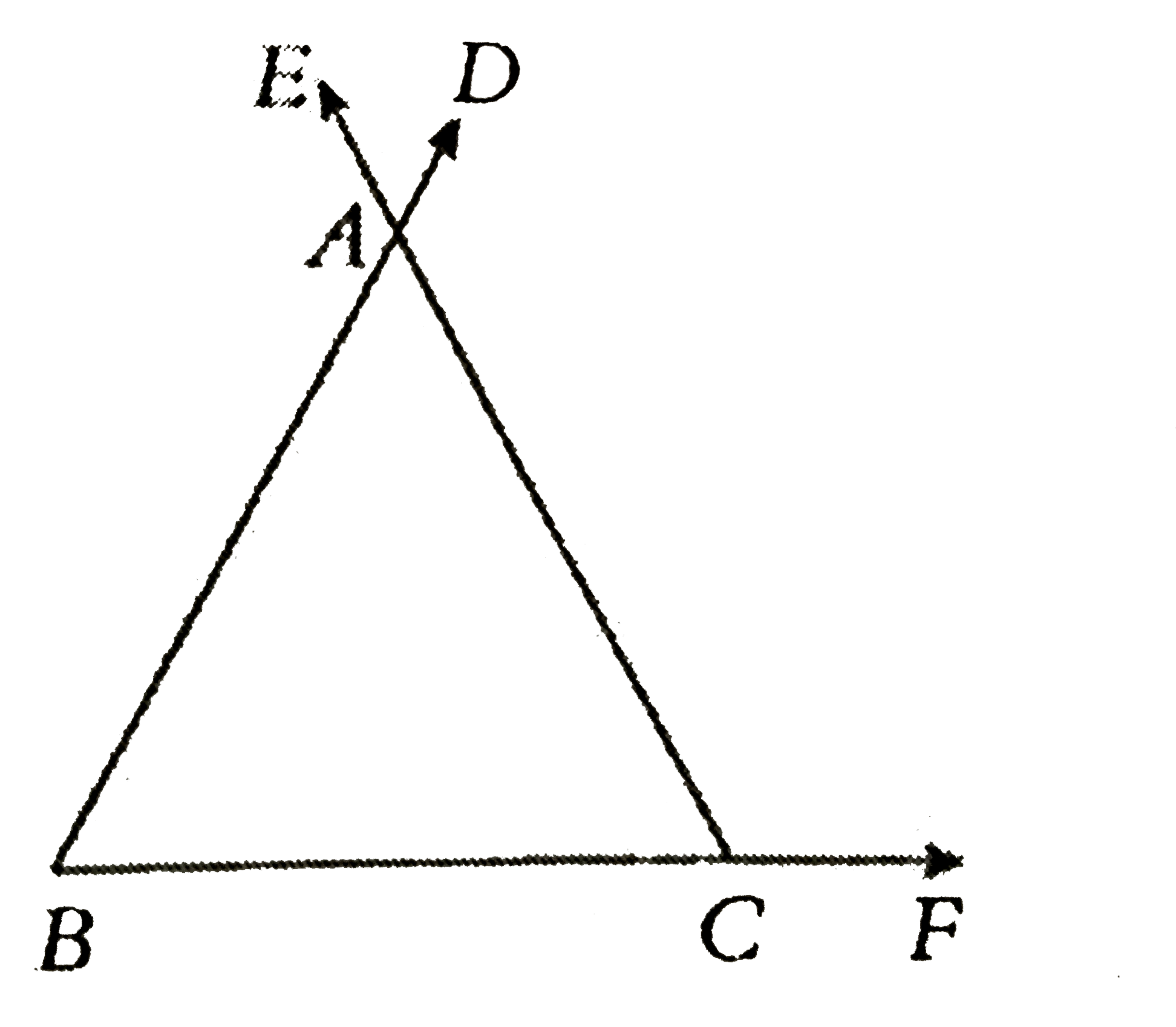
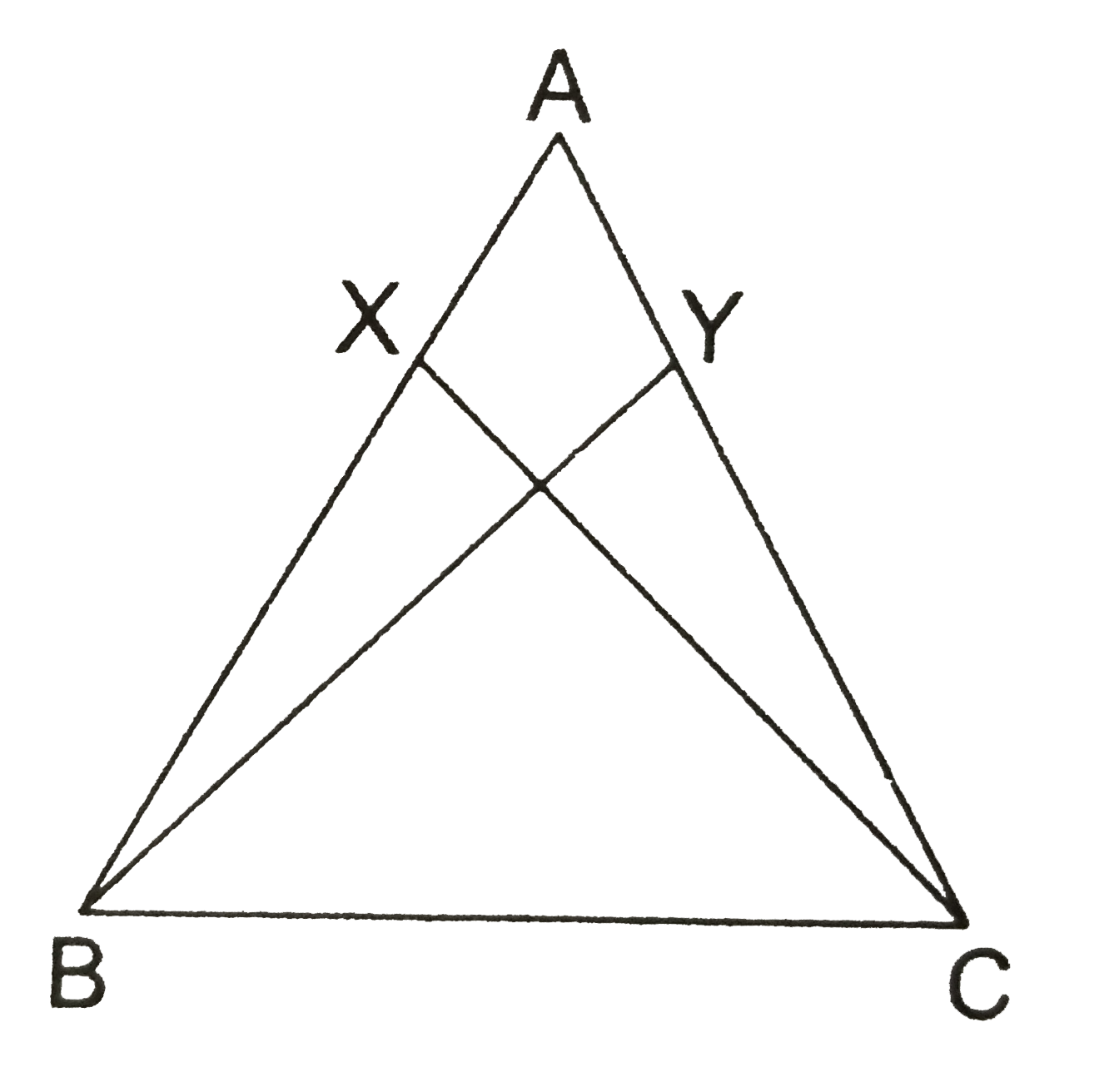
In the above figure ( not to scale ) the sides BA,BC and CA ofΔABC are produced to D,F, and E respectively such that ∠ACF=120∘ and ∠BAE=150∘. Then ∠ABC=_____.View SolutionIn the adjoining figure, X and Y are respectively two points on equal sides AB and AC of ΔABC such that AX = AY. Prove that CX = BY.
 View Solution
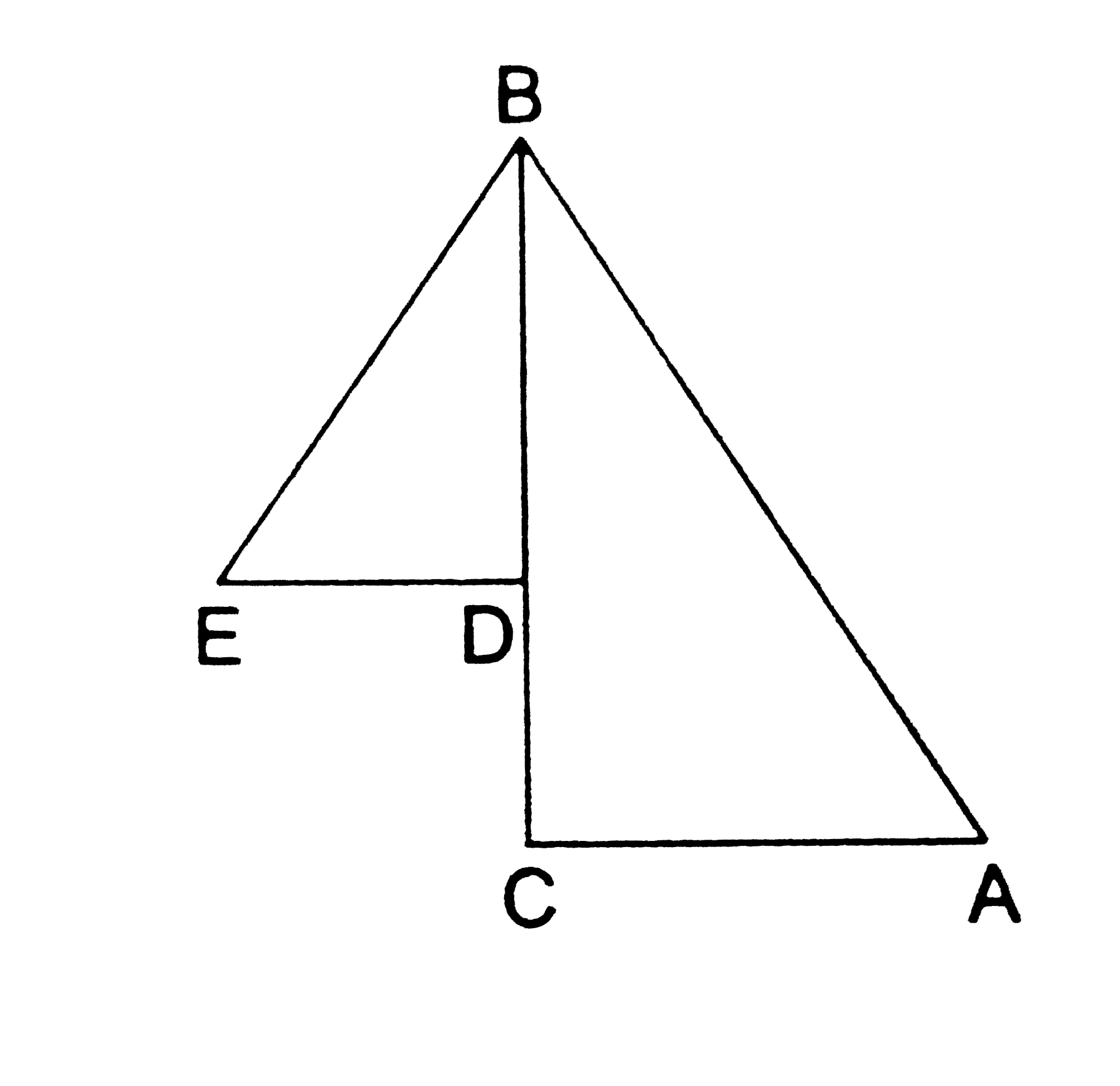
View SolutionIn the given figure, D is a point on side BC of a ΔABC and E is a point such that CD = DE.
Prove that AB+AC>BE.
 View Solution
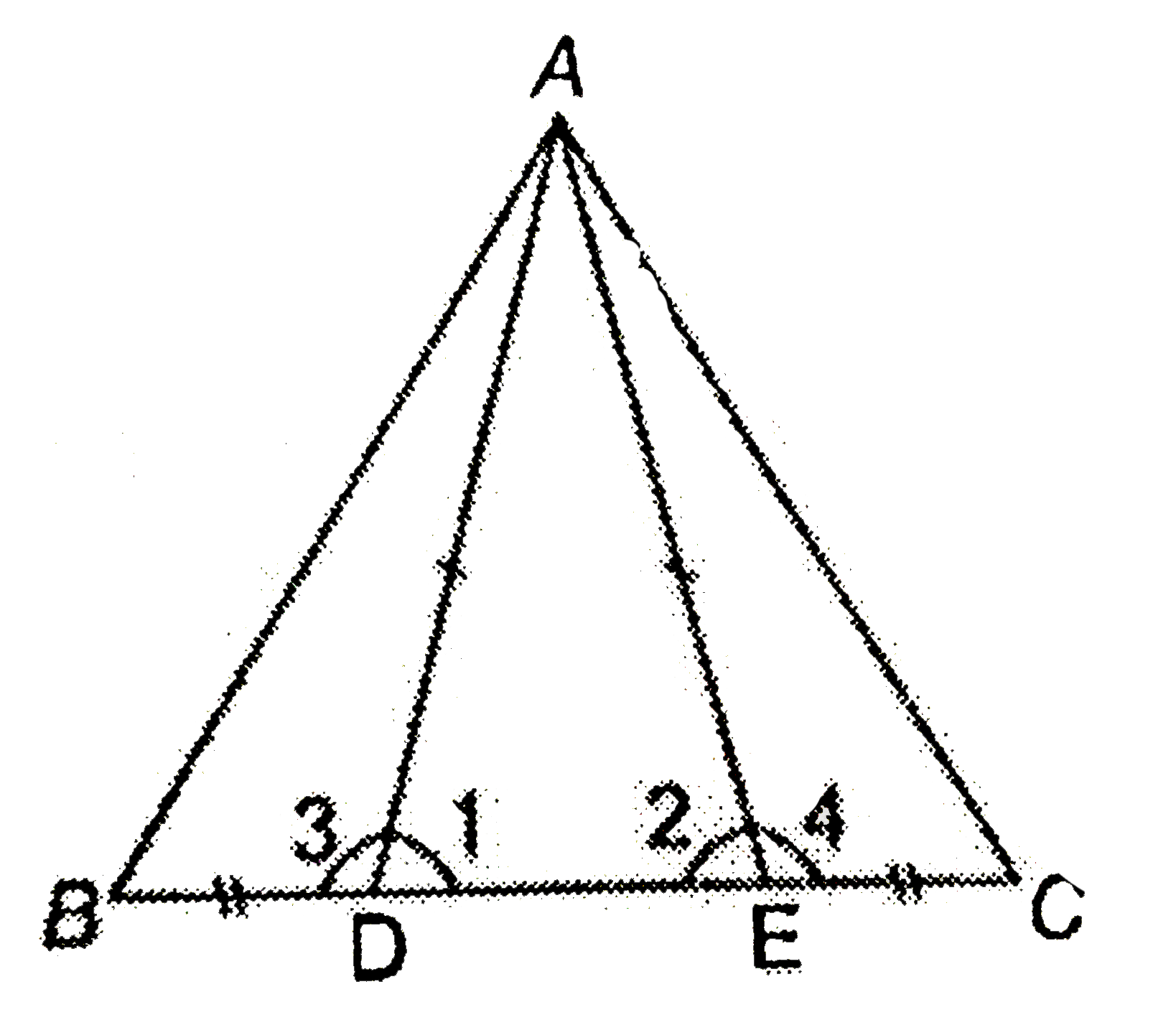
View SolutionIn the given figure, D and E are the points on the base BC of ΔABC such that BD=CE,AD=AE and ∠ADE=∠AED, prove that ΔADB≅ΔAEC.
 View Solution
View Solution

