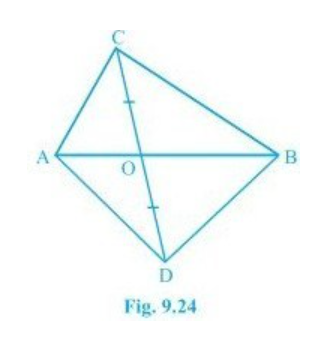
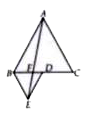
In figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O , show that ar(△ABC)=ar(△ABD).
Step by step video, text & image solution for In figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O , show that ar(triangleABC)=ar(triangleABD). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:NCERT SECTION ( EXERCISE 9.4)
Explore 19 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:EXERCISE ( Multiple Choice Questions )
Explore 45 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:NCERT SECTION ( EXERCISE 9.2)
Explore 7 Videos
- CIRCLES Book:MTG IIT JEE FOUNDATIONChapter:CIRCLES Exercise:OLYMPIAD/HOTS CORNER
Explore 6 Videos
Similar Questions
In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar(△ABC)=ar(△ABD)
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)= AODO
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
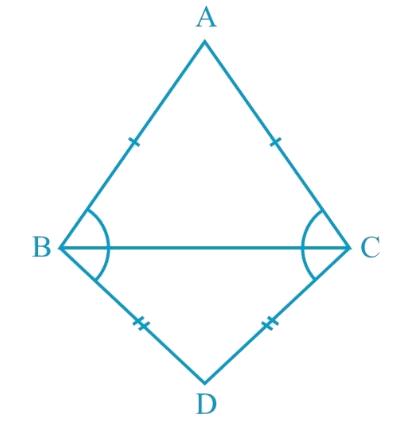
View SolutionIn Figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that ∠ABD=∠ACD
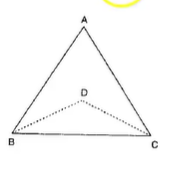
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
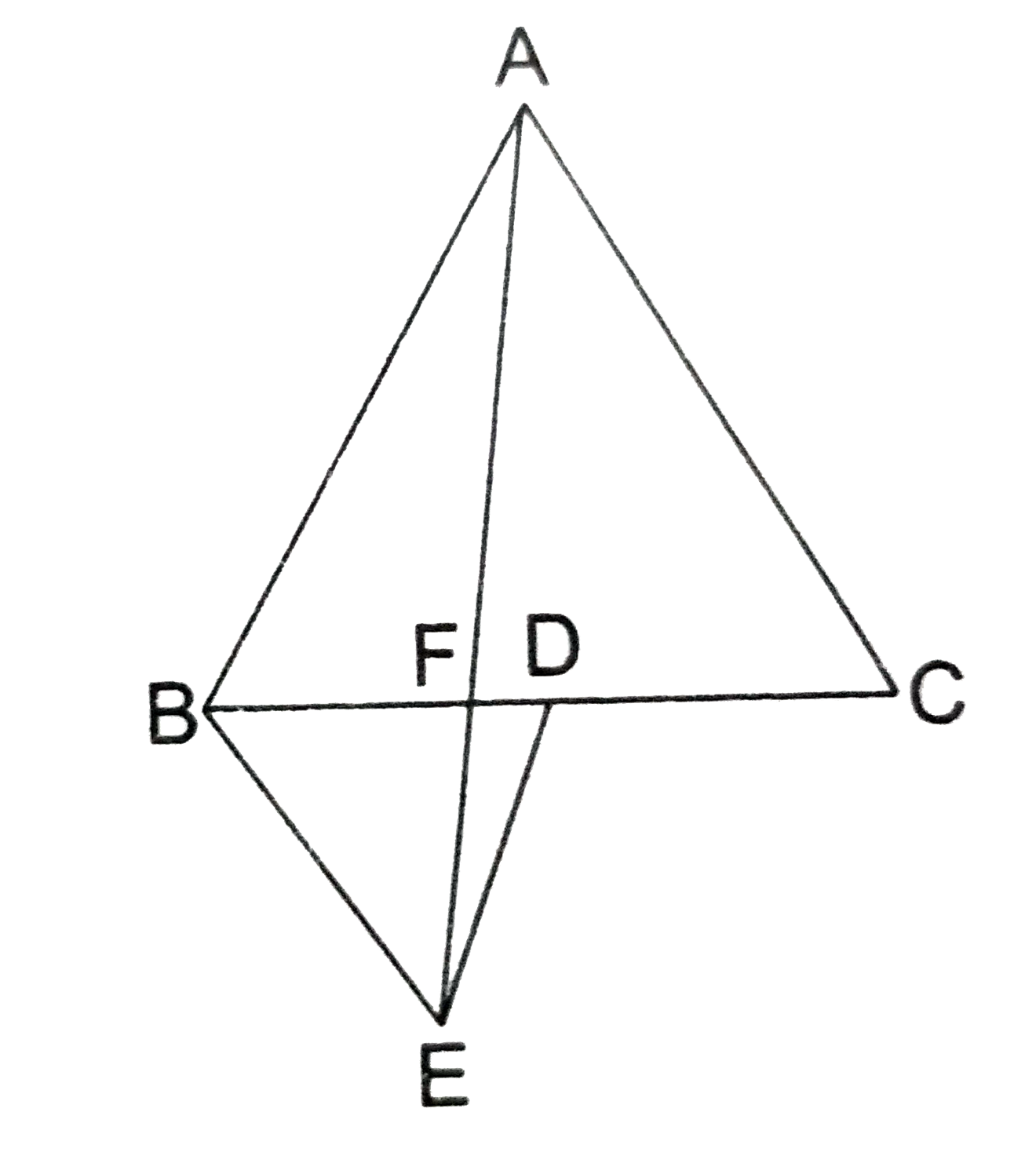
View SolutionIn Figure, ABC and DBC are two isosceles triangles on the same base BC such that AB=AC and DB=CD. Prove that ∠ABD= ∠ACD
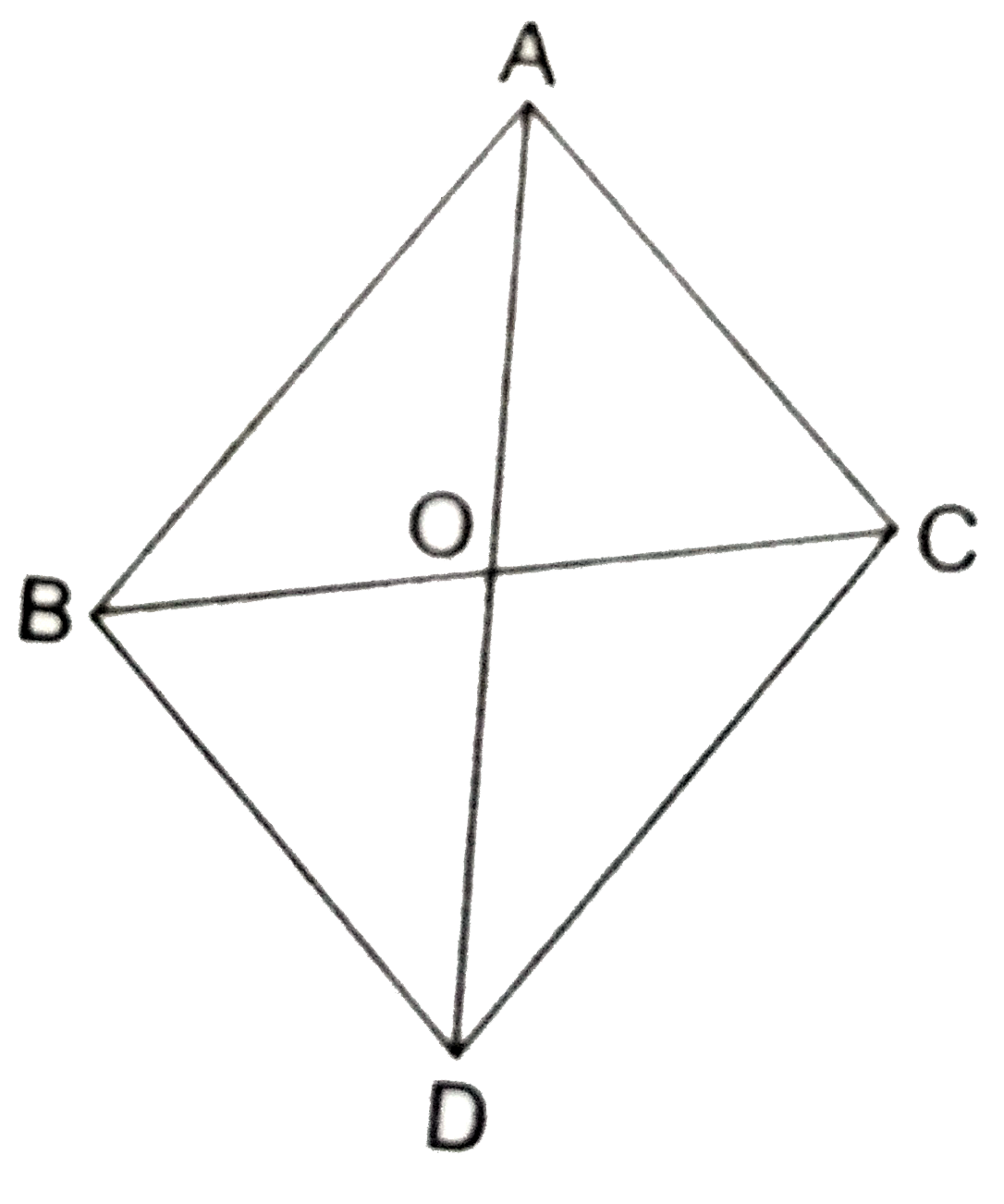
View SolutionIn the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
ar(ΔABC) = 2 ar(ΔBEC)
View Solution